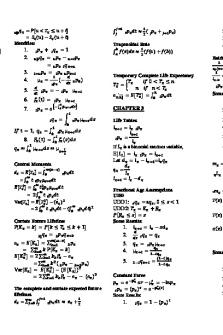Basic Financial Mathematics Formulas PDF

| Title | Basic Financial Mathematics Formulas |
|---|---|
| Course | Corporate Finance I |
| Institution | University of Sydney |
| Pages | 3 |
| File Size | 255.2 KB |
| File Type | |
| Total Downloads | 53 |
| Total Views | 187 |
Summary
This document provides a simplified break down of the first few weeks of Basic Financial Mathematics for FINC2011. I hadn't learned these in school so it helped me dramatically to break them into a simplified format, as the lectures provide a multitude of different variations of the same equations....
Description
Future Value and Present Value Time Value of Money
Assume the term structure of interest rate (discount rate/opportunity cost of capital/required rate of return) is flat. R (1) = R (2) = … R (n) 1. Simple Interest
2. Compound Interest (E.g. Annual compounding Interval)
3. Normal Future Value (at the end of N years) Of $PV invested at r% p.a. compounded M times a year
4. Continuous All other things equal; M & FV: Positively correlated M and FV: Negatively correlated When m approaches infinity
Present Value and Net Present Value Discounted Cash Flow
NPV Rule (Basic) NPV > 0 Accept NPV < 0 Reject
Usually C (0) < 0. Cn can be positive/negative/0
Perpetuities
Perpetuity Fixed payment at the end of each period, forever.
Perpetuity Due Fixed payment at the beginning of each period, forever.
Growing Perpetuity (Constant Growth Perpetuity/ Gordon Growth Model) Sometimes C (1) is not directly given, And you shall calculate C (1) as: C (1) = C (0) * (1 + g)
Annuities
Annuity Fixed payment at the end of Each period with each year ending at some point. Can be regarded as the difference Between one perpetuity starting now And another that starts N years later.
Equivalent Annuity Cash-Flow (Loan Payment) An amortised loan is a loan paid off in equal payments the loan payments can be viewed as an annuity. (e.g. Home mortgage loans and car loans) Solve for C, given r, n and PV
Annuity Due An annuity in which all the cash flows occur at the beginning of each period
Deferred Annuity An ordinary annuity that does not begin in one period’s time, but at a later date. Discounts Back (x – 1) periods this lump-sum amount in order to calculate the ordinary annuity’s PV.
Growing Annuity A growing perpetuity that Eventually comes to an end.
APR, ESIR, EAR and EIR
Annual Percentage Rate (APR) Indicates the nominal interest rate in one year without compounding (‘simple interest’) E.g. 10%p.a. compounded semi-annually = 5% per half-year or semi-annual period
Equivalent Simple Interest Rate (ESIR) Converting the compound interest rate into an equivalent simple interest rate.
Effective Annual Interest Rate (EAR) Accounts for the total amount of interest that is earned on both reinvested interest and principal over a year. Annual rate that takes into account the effect of compounding. Convert to compound rate.
Effective Interest Rate (EIR) Similar to EAR, but for a specific payment period and specific compounding period. M = number of compounding periods K = number of payment periods...
Similar Free PDFs

Basic mathematics
- 8 Pages

Basic integration formulas
- 1 Pages

Basic Derivative Formulas
- 1 Pages

Basic Mathematics-3300001
- 17 Pages

Basic Financial Concepts
- 19 Pages

Formulas for Financial Ratios-1
- 1 Pages

Financial Mathematics 1 & 2 Notes
- 178 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu