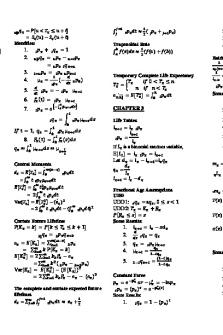Engineering Economics List of Formulas 2021 PDF

| Title | Engineering Economics List of Formulas 2021 |
|---|---|
| Course | Engineering Economy |
| Institution | University of Baguio |
| Pages | 2 |
| File Size | 70.2 KB |
| File Type | |
| Total Downloads | 66 |
| Total Views | 120 |
Summary
Prepared by Ron Mackinnon, University of British Columbia, © 2008. 7-Feb-EECE 450 — Engineering Economics — Formula SheetCost Indexes:Index valu eat timeBIndex valu eat timeA Cost at timeBCost at timeA=Power sizing:power-sizing exponentSize (capacity) of asset BSize (capacity) of asset A Cost ofasse...
Description
EECE 450 — Engineering Economics — Formula Sheet Ordinary Geometric Gradient Annuity:
Cost Indexes:
1 − (1 + g) n (1 + i) − n P= A1 ; i ≠ g i −g
Cost at time A Index value at time A = Cost at time B Index value at time B
Power sizing: Cost of asset A Size (capacity) of asset A = Cost of asset B Size (capacity) of asset B x = power - sizing exponent
x
Learning Curve: TN = Tinitial × N b log(learningcurve rate) b= log 2 TN = time to make N th unit Tinitial = time to make first unit N = number of finished units b = learning curve exponent
Simple Interest:
P=
nA1 ;i = g (1 + i)
(1+ i) n − (1+ g ) n F = A1 i −g
; i ≠ g
F = nA1 (1 + i) n−1; i = g A1 = payment in first period (end) g = periodic rate of growth P ,F ,i ,n as above for compound interest
Simple Annuity Due: 1− (1+ i) − n P= A (1+ i ) i n (1+ i ) − 1 F = A (1+ i ) i
Interest earned on amount P : I = Pin Maturity value : F = P (1 + in ) i = interest rate per time period n = number of time periods
Nominal, Periodic, Effective Interest Rates:
Compound Interest:
i=
F = P(1 + i) n F = future value P = present value i = periodic interest rate n = number of periods
Ordinary Simple Annuity:
A = cash amount (beginning of period) P ,F ,i ,n as above for compound interest r m
(
)m
(1+ ieff ) = 1+ rm r = nominal interest rate per year m = number of compounding periods per year ieff = effective interest rate (compounded annually) i = periodic interest rate
1 − (1 +i )− n P = A i
Equivalent Interest Rates:
(1 + i) n −1 F = A i A = periodic payment (end of period) P ,F ,i ,n as above for compound interest
ip = interest rate for payment period
Ordinary Arithmetic Gradient Annuity: 1 n Aeq = G − n i (1 + i) −1
(1+ i p ) p = (1 + ic ) c p = number of payment periods per year ic = interest rate for compounding period c = number of compounding periods per year
Ordinary General Annuity: 1− (1+ ip )− n = P A ip
Aeq = equivalent periodic payment
(1 + ip ) n −1 F = A ip ip = interest rate for payment period
G = gradient amount (periodicincrement)
n = number of payment periods
P ,i ,n as above for compound interest
P , F , A as above for annuities
(1+ i )n − in − 1 P =G 2 n i (1 + i)
Prepared by Ron Mackinnon, University of British Columbia, © 2008.
7-Feb-08
Perpetual Annuities: Ordinary : P =
A i
A A (1+ i ) = + A i i A Geometric Growth : P = ;i > g i− g P , A ,i , g as above for annuities Due : P =
Investment Criteria: CF1 CF2 CFn + + ... + n 1 2 (1+ r ) (1+ r ) (1 + r) NPV = net present value
NPV = CF0 +
NFV = CF0 (1 + r )n + CF1 (1 + r ) n −1 + ... + CFn NFV = net future value EACF = equivalent annual cash flow =
NPV −n 1 −(1 +r) r
CFj = cash flow at time j n = lifetime of investment r = MARR = minimum acceptable rate of return CF1 CF2 CFn 0 = CF0 + + + ... + (1 + i ) 1 (1 + i) 2 (1+ i) n i = IRR = internal rate of return PV(neg CFs, efin )× (1+ i′ ) n = FV(pos CFs, einv ) i ′ = MIRR= modified internal rate of return efin = financing rate of return einv = reinvestment rate of return PV(positive cash flows) Benefit - cost ratio, BCR = PV(negative cash flows)
Probability: E(X ) = Weighted average =
w1 S1 + + w kS k w1 + + wk
wi = weight for Scenario i S i = value of X for Scenario i E(X ) = µ X = expected value of X =
P(x j ) x j all j
Var(X ) = variance of X =
P(x j)( x j − µX )2 all j
P( x j ) = Probability( X = x j )
Depreciation: B= initial (purchase) value or cost basis S= estimated salvage value after depreciable life dt= depreciation charge in year t N= number of years in depreciable life t
Book value at end of period t: BVt = B −
di i =1
Straight-Line (SL): Annual charge: dt = (B – S)/N Book value at end of period t: BVt = B − t×d Prepared by Ron Mackinnon, University of British Columbia, © 2008.
Sum-of-Years’-Digits (SOYD): SOYD = N(N+1)/2 Annual charge: dt = (B − S)(N − t + 1)/SOYD Declining balance (DB): D= proportion of start of period BV that is depreciated Annual charge: dn = BD(1–D) n–1 n Book value at end of period n: BVn = B(1-D) Capital Cost Allowance (CCA): d= CCA rate UCC n= Undepreciated capital cost at end of period n Annual charge: CCA1 = B(d/2) for n = 1; CCAn = Bd(1–d/2)(1–d)n–2 for n ≥ 2 UCC at end of period n: UCCn = B(1–d/2)(1–d) n–1 BdT C 1 + i 2 PV(CCA tax shields gained) = i + d 1+ i
SdT C 1 PV(CCA tax shields lost) = i + d (1 + i )N TC = firm's tax rate; i = discount rate
Investment Project Cash Flows: Taxable income = OR−OC−CCA−I Net profit = taxable income ×(1−T) Before-tax cash flow (BTCF) = I+CCA+taxable income After-tax cash flow (ATCF) = Net profit + CCA + I = (Taxable income)×(1−T) + CCA + I = (BTCF − I − CCA)(1 −T) + CCA + I = (OR − OC)(1 −T) + I(T) + CCA(T) Net cash flow from operations = ATCF – I – DIV = (OR − OC)(1−T) + I(T) + CCA(T) − I − DIV = (OR − OC − I)(1−T) + CCA(T) − DIV = Net profit + CCA − DIV OR= operating revenue; OC= operating cost I= interest expense; DIV = dividends; T= tax rate Net cash flow = Net cash flow from operations + New equity issued + New debt issued + Proceeds from asset disposal − Repurchase of equity − Repayment of debt (principal) − Purchase of assets dT 1+ i 2 Net capital investment = B1 − C i + d 1+ i
dT 1 Net salvage value = S 1− C i + d (1+ i) N
Inflation: (1+i) = (1+i′ )(1+f) i = i′ + f + ( i ′)(f) i= market interest rate; i′ = real interest rate f= inflation rate
Weighted Average Cost of Capital (WACC): WACC =
D E × (1 − TC )id + × ie V V
V = D+E D= market value of debt; E= market value of equity V= market value of firm id= cost of (rate of return on) debt after-tax cost of debt: idt = id (1–T) ie= cost of equity 7-Feb-08...
Similar Free PDFs

Engineering-Economics
- 553 Pages

Geotechnical engineering formulas
- 34 Pages

Engineering Economics 6023
- 26 Pages

ENGINEERING ECONOMICS ret
- 11 Pages

Engineering Economics Reviewer
- 11 Pages

Mechanical Engineering Formulas AND REVI
- 162 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu