Límites trigonométricos PDF
| Title | Límites trigonométricos |
|---|---|
| Author | Valeria Gomez |
| Course | Matemáticas Discretas |
| Institution | Pontificia Universidad Javeriana |
| Pages | 7 |
| File Size | 473.3 KB |
| File Type | |
| Total Downloads | 62 |
| Total Views | 125 |
Summary
Límites trigonométricos y ejercicios de practica...
Description
1.6 Límites de funciones trigonométricas Los límites de las funciones trigonométricas se calculan mediante sustitución directa, siempre y cuando la función esté definida para el valor donde se quiere encontrar el límite. Así: Lím cos x x a
cos a
Lím cot x x a
cot a
Lím csc x x a
csc a
Recurso
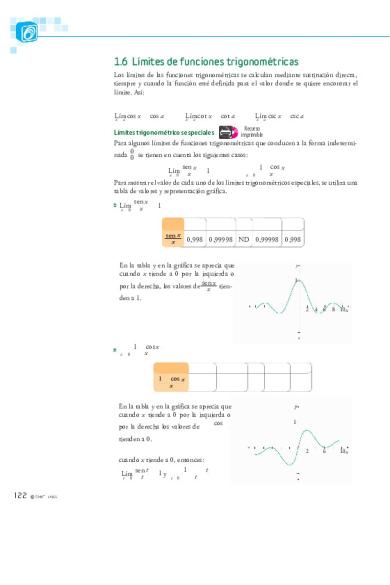
Límites trigonométricos especiales imprimible Para algunos límites de funciones trigonométricas que conducen a la forma indeterminada 0 0 se tienen en cuenta los siguientes casos: sen x 1 cos x Lím 1 x x x 0 x 0 Para mostrar el valor de cada uno de los límites trigonométricos especiales, se utiliza una tabla de valores y representación gráfica. sen x Lím 1 x x 0
sen x 0,998 0,99998 ND 0,99998 0,998 x En la tabla y en la gráfica se aprecia que cuando x tiende a 0 por la izquierda o sen x por la derecha, los valores de x tienden a 1.
y
1
2
1 x
0
4 6 8 10x
cos x x
1
cos x x
En la tabla y en la gráfica se aprecia que cuando x tiende a 0 por la izquierda o cos por la derecha los valores de
y 1
tienden a 0. 2
cuando x tiende a 0, entonces: 1 t sen t 1 y Lím t t t 0 t 0
1 22
©
6
10 x
Estándares Pensamientos numérico y variacional Actividad
EJEMPLOS sen 5 x 5 Lím x 0 5x
1. Determinar los siguientes límites. (2 cos x a. Lím x 0
3 tan x)
Finalmente, Lím x 0
Aplicando la sustitución directa, se obtiene: (
)
( )
Finalmente, Lím (2 cos x x 0
( )
3 tan x )
2
x tan 3 sec x Aplicando la sustitución directa, se obtiene: b.
x
x tan 3
sec x
2 3
tan
3 x
x 3
2
sec(
)
1
3
1 x
1
3
csc 2 x c. Lím sen x 2
Aplicando la sustitución directa, se obtiene: csc 2 2 sen 2
2 x Lím csc sen x
csc2
Finalmente, 2
1
2. Encontrar el valor del límite en cada caso. tan x a. Lím x x 0 tan x 0 Lím x tiene la forma 0 Se verifica la indeterminación. x 0 sen x tan x cos sen x Lím x Lím x x Se expresa tan x como cos x . sen x Lím x 0 x cos x sen x Lím x
Finalmente,
x
0
Se divide. 1 Se aplican propiedades cos x de los límites.
sen 5x b. Lím x x 0 Lím x 0
0 sen 5x x tiene la forma 0
Lím
sen 5x x
Lím
sen 5x 5x 5
Se verifica la indeterminación.
sen 5x x
5
sec x 1 0 Se obtiene una indeterminación al sustituir. 0 x sec x 1 cos x 1 cos x Se sustituye sec x por cos x x se resuelven las operaciones. cos x 1 cos x x x 0 Se simplifica y se aplica límite sec x 1 Finalmente, x 0 x sec x trigonométrico especial. 0
3. Comprobar la existencia del siguiente límite. x (3 x2 5 x) 2x x (3 x 2 x
0
Lím x
tan x x
5
sen 3x c. Lím x 0 sen 4x sen 3x 0 Se verifica la indeterminación Lím tiene la forma 0 x 0 sen 4x al sustituir. sen 3 x Se divide por x, el numerador x Lím y el denominador. sen 4x x sen 3x 3 3x Lím Se complifica 3 y 4, respectivamente. sen 4 x 4 4x sen 3x 3 Lím 3x x 0 Se aplica propiedad de los límites. sen 4 x 4 Lím 4x x 0 3 ( 1) 3 Se aplica límite trigonométrico especial. 4 ( 1) 4 sec x 1 d. x x sec x x
x
5 (1 )
0
5 x) 2 x2
x
Se obtiene 00 al realizar la sustitución.
3x 2 5x sen x Se aplica propiedad Lím 2x x 0 de los límites. 3x 5 Se simplifica y se aplica límite ( ) 2 trigonométrico especial.
5 2( ) 5 2 Lím 0
(3x 2
5x ) sen x 5 existe y es igual a 2 . 2x 2
©
123
Responde las siguientes preguntas. 93. ¿Cómo se evitan indeterminaciones en los límites de funciones racionales?
Responde V, si el enunciado es verdadero o F, si es falso. Justifica tu respuesta. 104. Si Lím f (x ) x a
94. ¿Cuál es la diferencia al racionalizar funciones radicales si el índice es de orden 2 o de orden 3? 95. ¿Para qué valores de a Lím (tan x) no existe? x a Determina el valor de los siguientes límites racionales. 2x 2 x 1 96. Lím 2 x 2x 3 x 2 8x 15 97. xLím3 x x 12 2 2 x 98. xLím 2 5x 3 x x 6 x 2 11 x 30 99. x2 2x 35 6x 3 7 x 100. x 0 8x 9x 2 x 16 101. Lím x 4 x x 12 x 3 2x 2 9x 18 102. Lím x 2 x3 8 103. Encuentra y corrige los errores que se cometieron en la resolución del siguiente límite. Lím
2
x
3
2x
1
2 3
x 2x
1
2 2
x 3 x 3
2x 2x
4 x 3 2x ( 9 ( 2x 1)) 2 4 (9
x 3 2x 2x 1) 2
4
2x 1 x 3 2 (4 x) 2 x
3
2x 2
3 2
1 x
9 4
1 x
6 4
3 2
1 x
Se aplica suma por diferencia. Se eliminan paréntesis.
Se factoriza. Se simplifica.
105. Toda indeterminación de la forma 0 0 se puede evitar mediante factorización. ( ) sen ( mx) nx cero. ( )
108. Determina, si existe, el límite f (x h ) f (x ) h h 0 Asocia cada límite con su respectivo valor. 109.
1 x
©
x
x 111. Lím
2 x2 x
114.
3x x 1 x 3 49
3
1 Lím
1
x
x
1
b. 0 c. 3
x 1 2
1 5 8x x 1 3 x 1
1 56
a.
x
0
5 16
d.
2 1
e. 1 f. Lím x 0
sen x x 1
1 2 1 para de-
cos x x (sugerencia: multiplica numerador y denomimostrar formalmente que
x
0
Encuentra el valor de los siguientes límites trigonométricos. tan2 3x sen 4x 116. Lím x 119. Lím 2 x 0 x cos 2x 2 1 cos 3x x x cos 5x 117. Lím 120. sen 4 x x 0 5x cos x 1 cos2 x 121. 118. Lím cot x 3x x 0 2
1 24
m n , con m y n diferentes de
106. Lím x 0
1 1
Se multiplica por los conjugados.
0 entonces
f (x ) Lím g (x ) existe. ( )
112.
Límite dado.
0 y Lím g (x) x a
Estándares Pensamientos numérico y variacional
1.7 Límites infinitos
Enlace web
En algunos casos, cuando se evalúa el límite de una función para un valor dado, se encuentra que la función crece o decrece sin cota. En este caso, se concluye que el límite de la función no existe. Para expresar que los valores de f (x) crecen sin cota cuando x se acerca a c se escribe Lím f (x ) . x c De igual manera, si los valores de f (x) decrecen sin cota cuando x se acerca a c se escribe Lím f (x ) . x c
Recuerda que… , La igualdad no e límit el significa que existe porque el símbolo número real. Este símbolo indica el comportamiento de f(x) cuando x tiende a c.
Una cota es un número que es mayor o menor que todos los elementos de un conjunto dado.
EJEMPLOS 1. Realizar una tabla de valores y analizar el comportamiento de la función 2x 1 f (x) x 3 Para algunos valores de x, se construye la siguiente tabla. x
2,9
2,99
2,999
2,9999
3
3,0001 3,001
3,01
3,1
2x 1 x 3 En la tabla, se aprecia que para valores cercanos a 3 por la izquierda, la función decrece sin cota y se expresa como: 2x 1 x 3 x 3
y 20 15 10
Mientras, que para valores cercanos a 3 por la derecha, la función crece sin cota y se expresa 2x 1 como x 3 x 3 . La representación gráfica de permite apreciar con mayor 2x comportamiento de f (x) x x tiende a 3.
5 0
3
6
9
12 x
la función claridad el 1 3 , cuando
2. Elaborar una tabla de valores e indicar si la función crece o decrece sin cota, utilizando xLím2 2 2 . x 4
2 4 2 x2 4 Es decir, Lím2 Lím2
x2
2 4
. Finalmente, xLím
x2
2 4
no existe. ©
125
1.8 Límites en el infinito Historia de las matemáticas
Ampliación multimedia
Si la variable x crece o decrece sin cota y la función f(x) se aproxima a los valores L y M, respectivamente. Estos límites se llaman límites en el infinito y se expresan como: Lím f (x )
x
Henri Poincaré
L
Lím f (x )
M
(1854-1912)
al eje x, exista un número más grande que todos al cual se aproxima x. En lugar de esto, Para calcular límites en el infinito se tienen en cuenta los siguientes casos: k k yx x xn xn kx n y xLím kx n y si n es impar, Lím kx n y xLím kx n par, Lím x x
.
EJEMPLOS Poincaré fue un extraordinario matemático, físico y filósofo. Se le considera el último matemático universalista. “Una especie de poeta del infinito”.
8 x Para calcular los límites, se tiene en cuenta la siguiente tabla para algunos valores de x. 1. Hallar Lím f (x) y Lím f (x) , si f (x) x
f (x )
8 x
8 Cuando x toma valores cada vez más grandes pero negativos, la función f (x ) x tiende a 0. Cuando x toma valores cada vez más grandes pero positivos, la función f (x) 8 x tiende a 0. 8 8 Se escribe: 0y . x x 2. Una población de pingüinos crece en un ambiente de confinamiento de acuerdo con la curva de crecimiento logístico que se muestra en la figura. En esta, C es la capacidad de sostenimiento del ambiente y representa la cantidad máxima de individuos que pueden ser sostenidos en ese ambiente. P(t) C
ta
Recuerda que… Los límites infinitos y los límites en el infinito no se calculan mediante sustitución directa.
1 26
©
t
Plantear un límite que determine la capacidad de sostenimiento del ambiente habitado por los pingüinos. En este caso, la función población de pingüinos P depende del tiempo t. Es decir, P(t). P (t) C . Luego, el límite que determina la capacidad del ambiente esLím t
Estándares Pensamientos numérico y variacional Actividad
Límites en el infinito de una función racional En algunos límites de funciones racionales se presenta la indeterminación la variable x crece o decrece sin cota.
, cuando
Recuerda que… Una indeterminación de
Para determinar el límite de estas funciones, se dividen el numerador y el denominador de la función racional entre la potencia de mayor grado. A partir de este proceso se puede presentar. P (x) Q( x)
Si el grado de P(x) es mayor que el grado de Q(x).
P (x) Q( x)
Si el grado de P(x) es menor que el grado de Q(x).
P (x) Q( x)
m n
suelve efectuando la resta de func iones. Cuan do aparecen radicales se multiplica y se divide por la expresión conjugada.
Si el grado de P(x) y Q(x) son iguales donde m y n son los coeficientes de los términos de mayor grado de P(x) y Q(x), respectivamente.
EJEMPLOS c.
Determinar el valor de cada límite. 3x5 5 x3 12 x5 8 x 4 6x Al aplicar el criterio se obtiene: 3 x 5 5 x3 12 Lím 5 x 8 x4 6 x a. Lím x
Lím
x4 x3
7x2 8x
15 2
x
3 1
81x 6
3
15 2
9x 3
1
81x 6
Límite dado. 9x 3
1 81
( 81x 6 1) 81x 6 1 1 81x6 1
x4 4 Lím x 3 x x4
1 0 7x2 8x
1 x 0 0 15 2
7 x2 x4 8x x4
15 x4 2 x4
7 15 x2 x4 8 2 x x 0 1 0 0 .
81x6 1 9
81x 6 9x 3 9x3
1
9 x3
Se efectúan las operaciones. Se simplifica.
que el grado del denominador. x d. Lím 8 x
4 5x
x 4 Lím 8 5 x
Límite dado.
x
1
x4 Lím x x
9 x3
1
resuelve multiplicando y dividiendo por el conjugado.
Otra forma de calcular el límite es dividir el numerador y denominador entre la mayor potencia. Así: 3 x5 5x 3 12 5 5 3x5 5x3 12 x x x5 Lím 5 Lím 5 x 8 x4 6x x 8x4 6x x5 x5 x5 5 12 3 x2 x5 8 6 1 x x 3 0 0 3 1 0 0 1 x4 7 x2 b. Lím x 3 8x
81x6
x
x2 x 8 x
4 x2 5x x
1 8 x
4 x 5
1 0 0 5 Finalmente,
Se dividen el numerador y el denominador entre la mayor potencia.
Se simplifica. 1 5 x 8
1 5 4 5x
1 5.
©
127
Expresa con tus palabras el significado de las siguientes expresiones. 122. Lím f (x ) x 123. xLím f (x )
M
124. Lím f (x ) x a
L
125. Lím f (x ) x a
Determina, en caso de existir, el valor de los siguientes límites. Justifica tus procedimientos. 1 1 126. Lím x 1 x x 127. Lím x
x2
6x x 5
x
7
6,9
6,99
2 9x 7
7,001
141. Lím f (x ) x 0 142. Lím f (x ) x 0
Observa las gráficas de las funciones exponenciales y, luego, responde. y
y
145. x
x
132. ¿Cómo debe ser el valor de a para que se cumpla la condición xLím ax 0? Lím 3 x
x
sus límites al infinito existe? Si f(x) es una función acotada (es decir, existen consf ( x) x
x
sen x x
136. Determina el valor de Lím x
0. 5 cos x . x
.
y Lím f ( x) x
0
Analiza los siguientes límites. 8 4 4x 143. Lím 3 x 7 2 x5 146. Lím x 2 x x x 0 4x 2x 3 144. Lím x 1 x 1
©
7,01
Encuentra una función que cumpla las condiciones propuestas en cada caso.
x 4 5 x2 8 131. Lím 2 4x 1
1 28
7,1
140. ¿Qué se puede afirmar acerca de xLím f (x ) , 7 Lím f ( x ) y Lím f ( x ) ? 7 x 7
5 x 3x
135. Demuestra que xLím
6,999
y
x 4 3 x7 x 128. x 4 x x6 5x 1 129. Lím x x2 130. x
Sean f y g funciones polinomiales. f ( x) 137. ¿En qué condiciones Lím g ( x) existe? f (x ) g ( x) 138. Si Lím g ( x) y Lím existen; ¿cómo son f f (x ) y g? 4x Considera la función y f ( x) x 49 139. Completa la siguiente tabla.
x
5
3x 2 1 x 5
147. 148.
1 2
x x
5 9 1
1
x
Lee y resuelve. 149. Se ha estimado que la población de zorros alrededor de una granja se rige por la 100 (6 t2 3) fórmula z , 2 t donde t viene dado en meses. Conforme transcurre el tiempo, ¿qué ocurrirá con el tamaño de la población? 150. Según la teoría de la relatividad de Einstein, la masa M de un cuerpo depende de su velocidad v mc y dicha relación viene dada por M c2 v2 donde m es la masa del cuerpo en reposo y ocurre con el cuerpo a medida que su velocidad se acerca a la de la luz?...
Similar Free PDFs
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu
