AMP1514 Assignment 01 solutions PDF

| Title | AMP1514 Assignment 01 solutions |
|---|---|
| Author | Karin Louw |
| Course | Mathematical Modeling |
| Institution | University of South Africa |
| Pages | 10 |
| File Size | 181 KB |
| File Type | |
| Total Downloads | 866 |
| Total Views | 958 |
Summary
BAR CODELearn without limits. universityof south africaTutorial Letter 201/0/Mathematical ModellingAPMYear moduleDepartment of Mathematical SciencesSolutions to Assignment 01APM1514/201/0/APM1514-TL-201 SolutionsQuestion 1 [20 marks]1 Autonomous. Not First Order. 1 Autonomous. Not First Order. 1 Aut...
Description
APM1514/201/0/2021
Tutorial Letter 201/0/2021 Mathematical Modelling
APM1514 Year module Department of Mathematical Sciences
Solutions to Assignment 01
BAR CODE
Learn without limits.
university of south africa
APM1514-TL-201 Solutions Question 1 [20 marks] 1.1 Autonomous. Not First Order. 1.2 Autonomous. Not First Order. 1.3 Autonomous. Not First Order. 1.4 Autonomous. First Order. 1.5 Autonomous. First Order. 1.6 Autonomous. First Order. 1.7 Autonomous. Not First Order. 1.8 Autonomous. Not First Order. 1.9 Autonomous. Not First Order. 1.10 Autonomous. First Order. Question 2 [16 marks] 2.1 P (n + 1) = (1)n+1P (n). Given that P (0) = 3. ∴ P (1) = (1)0+1P (0) = 3 ∴ P (2) = (1)1+1P (1) = 3 ∴ P (3) = (1)2+1P (2) = (3) = 3 ∴ P (4) = (1)3+1P (3) = 3 2.2 P (n + 1) = P (n) + sin(nπ). Given that P (0) = 0. ∴ P (0) = 0 ∴ P (1) = 0 + sin(0π) = 0 ∴ P (2) = P (1) + sin(π) = 0 ∴ P (3) = P (2) + sin(2π) = 0 ∴ P (4) = P (3) + sin(3π) = 0
2.3 P (n + 1) =
p
P (n). Given that P (0) = 4.
1
∴ P (1) = | ± 2| = 2 We consider only the positive input in the recursive updating and not the imaginary solution: p p ∴ P (2) = P (1) = 2 p 1 ∴ P (3) = P (2) = 24 1
∴ P (4) = 28
2.4 P (n + 1) = P (n)[P (n) 1]. Given that P (0) = 2. ∴ P (1) = P (0)[P (0) 1] = 2 ∴ P (2) = P (1)[P (1) 1] = 2 ∴ P (3) = P (2)[P (2) 1] = 2 ∴ P (4) = P (3)[P (3) 1] = 2 2.5 P (t) = ln |10 cos(π nt )|, where, t = 0, 1, . . . , n, and n 2 N. ∴ P (0) = ln |10 cos(π n0 )| = ln 10, 8n 2 N ∴ P (1) = ln |10 cos(π n1 )| for n = 2 we have P (1) as undefined and generally approaches ln 10 as n ! 1. ∴ P (2) = ln |10 cos(π n2 )| for n = 4 we have P (2) as undefined and generally approaches ln 10 as n ! 1. ∴ P (3) = ln |10 cos(π n3 )| for n = 6 we have P (3) as undefined and generally approaches ln 10 as n ! 1. ∴ P (4) = ln |10 cos(π n4 )| for n = 8 we have P (4) as undefined and generally approaches ln 10 as n ! 1. 1
2.6 P (t) = t−2 e− t . ∴ P (0) is undefined. P (1) = e−1 . P (2) = 4√1e . P (3) = 2.7 P (n + 1) =
n+1 P (n) n!
+ 2, given that P (0) = 1. 2
1 √ . 9 3e
P (4) =
1√ . 16 4 e
∴ P (1) = 11 P (0) + 2 = 3, ∴ P (2) = 12 P (1) + 2 = 8, ∴ P (3) = 23 P (2) + 2 = 14. ∴ P (4) = 64 P (3) + 2 = 1 nn
2.8 P (n + 1) =
34 . 3
+ (n2 n)2−n , given that P (0) = 1.
∴ P (1) is undefined, ∴ P (2) =
1 1
+ (0) = 1,
∴ P (3) =
1 4
+
∴ P (4) =
1 27
2 4
= 34 .
+ (3) 41 =
85 . 108
Question 3 [6 marks] 3.1 an+1 = 3an + 1, We first evaluate a1 , a 2 , a3 , by using a0 : a1 = 3a0 + 1, a2 = 3[3a0 + 1] + 1 = 32 a0 + 3 + 1, a3 = 3[32 a0 + 3 + 1] + 1 = 3 3 a0 + 32 + 3 + 1. In general we obtain: n
an = 3 a0 + 3 n−1 + . . . + 1 = 3n a0 +
n−1 X
3n ,
n=0
3n 1 3n 1 n an = 3 a0 + = 3 a0 + . 31 2 n
3.2 an+1 = an2 10,
3
We first evaluate a1 , a 2 , a3 , by using a0 : a1 = a02 10, a2 = [a02 10]2 10, 2 a3 = [a02 10]2 10 10.
In general we obtain a nested solution given by: i2 h 2 an = . . . [a02 10]2 10 10 . . . 10. | {z } (n−1)times
3.3 = Pt , Z Z dP dt = , P t dP dt
ln |P | = ln |t| + b, let A = eb , Therefore, the general solution is P =
A t
3.4 dP dt
Z
= (1 + 2P ), Z 2.dP = 1.dt, 1 + 2P
1 2 1 ln |1 + 2P | = t + a, 2 let b = 2a, ln |1 + 2P | = 2t + b, let C = eb , 1 + 2p = e−2t+b 1 + 2p = Ce−2t 4
Thus, the general solution is p = 21 + De−2t , where D =
C 2
.
Question 4 [10 marks] 4.1 P (n + 1) =
P (n) , 3
with P (0) = 2,
We first evaluate P (1), P (2), P (2), by using P (0) = 2: P (1) =
P (0) 2 = , 3 3
P (1) 2 = 2, 3 3 2 P (2) = 3. P (3) = 3 3 Therefore, the particular solution is P (2) =
P (n) =
P (0) 2 = n. n 3 3
4.2 P (n + 1) = P (n) + 2, with P (0) = 1, We first evaluate P (1), P (2), P (2), by using P (0) = 1: P (1) = P (0) + 2 = 1, P (2) = (P (0) + 2) + 2 = P (0) + 2(2) = 5, P (3) = P (0) + 2(3) = 7. Therefore, the particular solution is P (n) = P (0) + 2n = 1 + 2n. Question 5 [20 marks] 5.1 1, 2P P = 0 P (1, 2 1) = 0 5
0, 2P = 0 P =0 Only one equilibrium pont exists at zero. 5.2 P = 0, 2P + 1 0, 8P = 1 5 P = = 1, 25 4 Only one equilibrium pont exists at 1,25. 5.3 P = P 2 2P 2 P 2 3P 2 = 0 p 3± 9+8 P = 2
P1 =
√ 3+ 9+8 , 2
or P2 =
√ 3− 9+8 2
Thus, two equilibrium ponts exist. 5.4 P4 P = 0
P (P 3 1) = 0
P (P 1)(P 2 + P + 1) = 0 P = 0, or P = 1 or √ P = −1± 2 1−4 , this P however has no solution. Therefore, only solutions P = 0 and P = 1, are regarded as equilibrium ponts that exist. 5.5
p p p p 2 P = P P p p p P ( P 2) = 0 p p p P = 0, or P = 2 P = 0, or P = 2 6
Therefore, solutions P = 0 and P = 2, are equilibrium ponts that exist. Question 6 [16 marks] 6.1 P (n + 1) = P (n), P (1) = P (0), P (2) = P (1) = (P (0)) = P (0), P (3) = P (2) = P (0), The general solution is P (n) = (1)n P (0). 6.2 P (n + 1) = 5P (n), P (1) = 5P (0), P (2) = 52 P (0), P (3) = 53 P (0), The general solution is P (n) = 5n P (0). 6.3 P (n + 1) = 0, 01P (n), P (1) = (0, 01)P (0), P (2) = (0, 01)2 P (0), P (3) = (0, 01)3 P (0), The general solution is P (n) = (0, 01)n P (0). 6.4 P (n + 1) = 0, 2P (n), P (1) = (0, 2)P (0), P (2) = (0, 2)2 P (0), P (3) = (0, 2)3 P (0), 7
The general solution is P (n) = (1)n (0, 2)n P (0). 6.5
1 P (n + 1) = P (n), 8 1 P (1) = P (0), 8 ✓ ◆ 1 P (2) = 2 P (0), 8 ✓ ◆ 1 P (3) = 3 P (0), 8
The general solution is P (n) =
✓
◆ P (0) . 8n
Question 7 [12 marks] 7.1 P (n + 1) = P (n), with P (0) = a5, Assume that a 6= 0 and let r = 1 (meaning it is not r > 0): ✓ ◆ 5 n , P (n + 1) = (1) a such that as n ! 1, for a > 0, we have 8 5 > < f or n 2 even ! , a P (n + 1) ! > : f or n 2 odd ! 5, a OR
for a < 0, we have
8
8 5 > < f or n 2 even ! , a P (n + 1) ! > : f or n 2 odd ! 5. a
Therefore, the solution diverges to the value ± a5 depending on your initial assumption of a. 7.2 P (n + 1) = 2P (n), with P (0) = 1, Let r = 2: P (n + 1) = 2n (1) As n ! 1, we have P (n+1) ! 1. Meaning that the solution grows without bound. 7.3 P (n + 1) = 41P (n), with P (0) = 2, Since r =
1 4
satisfies the inequality: 0 < r < 1. ✓ ◆n 1 (2) P (n + 1) = 4
Therefore, as n ! 1, we have P (n + 1) ! 0. Meaning that the solution converges to zero.
9...
Similar Free PDFs

AMP1514 Assignment 01 solutions
- 10 Pages

Assignment Solutions-Set 01
- 5 Pages

01 instructors solutions manual
- 32 Pages

IFEM Tutorial 01 Solutions
- 10 Pages

Tutorial Solutions 01
- 2 Pages

Tutorial 01 Solutions
- 2 Pages

Assignment Solutions
- 29 Pages

Assignment 01 1 - asdfad
- 1 Pages

Assignment 01 Solution
- 3 Pages
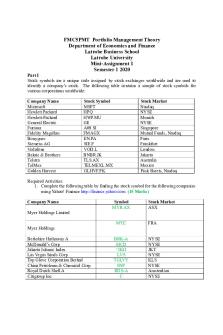
Mini-Assignment 01-FMC5PMT
- 4 Pages

Assignment 01 0 - aloooo
- 2 Pages

Study Guide 01-02 - Solutions
- 31 Pages

ELEC3111-Assignment-01
- 2 Pages

CS Assignment 01
- 2 Pages

Design Pattern(Assignment 01)
- 5 Pages

Statistic Group Assignment 01
- 32 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu