Analytic Geometry Problems with Solutions PDF

| Title | Analytic Geometry Problems with Solutions |
|---|---|
| Author | Palada Royce |
| Course | BS EE |
| Institution | Eastern Samar State University |
| Pages | 8 |
| File Size | 412.5 KB |
| File Type | |
| Total Downloads | 93 |
| Total Views | 173 |
Summary
Review materials...
Description
Visit For more Pdf's Books Pdfbooksforum.com
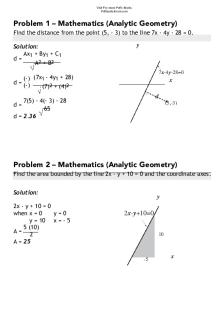
Problem 1 – Mathematics (Analytic Geometry) Find the distance from the point (5, - 3) to the line 7x - 4y - 28 = 0. Solution: Ax1 + By1 + C1 d= A2 + B2
y
7x-4y-28=0
(-) (7x1 - 4y1 + 28) d = (-) (7)2 + (4)2
x d
7(5) - 4(- 3) - 28 d= 65 d = 2.36
(5,-3)
! ! ! ! ! !
Problem 2 – Mathematics (Analytic Geometry) Find the area bounded by the line 2x - y + 10 = 0 and the coordinate axes. Solution: 2x - y + 10 = 0 when x = 0 y=0 y = 10 x = - 5 5 (10) A= 2 A = 25 ! ! ! ! ! !
y
2x-y+10=0 10
-5
x
Visit For more Pdf's Books Pdfbooksforum.com
Problem 3 – Mathematics (Analytic Geometry)
Find the slope of the line whose parametric equations are x = 4 t + 6 and y = t - 1.
Solution: t=x+1 y = 2 (x + 1) y = 2x + 2 y = mx + b m=2
! ! !
Problem 4 – Mathematics (Analytic Geometry)
A line has a slope of 3 and a y-intercept of 8. passes through point (-2, y). Find the value of y. Solution: y = mx + b y = 3x + 8 y = 3 (-2) + 8 y=2 ! ! !
It
Visit For more Pdf's Books Pdfbooksforum.com
Problem 5 – Mathematics (Analytic Geometry) Determine the length of the x2 + y2 - 4x - 5 = 0 from (8, -2).
tangent
to
the
circle
y
Solution: x2 - 4x + 4 + y2 - 5 = 4 (x - 2)2 + (y - 0)2 = 0 t2 = x2 + y2 - 4x - 5 t2 = (8)2 + (-2)2 - 4 (8) - 5
t x
(2,0)
t = 5.57
(8,-2)
! ! ! ! ! ! ! ! !
Problem 6 – Mathematics (Analytic Geometry) Determine the equation of the radical axis of the circles x2 + y2 18x - 14y + 121 = 0 and x2 + y2 - 6x + 6y + 14 = 0. Solution: x2 + y2 - 18x - 14y + 121 = 0 x2 + y2 - 6x + 6y + 14 = 0 - 12x - 20y + 107 = 0 12x + 20y - 107 = 0 ! ! !
Visit For more Pdf's Books Pdfbooksforum.com
Problem 7 – Mathematics (Analytic Geometry) Determine the length of the latus rectum of the parabola x2 - 6x - 12y - 51 = 0. y
Solution: x2 - 6x + 9 = 12y + 51 + 9 (x - 3)2 = 12y + 60 (x - 3)2 = 12 (y + 5)
x
(0,0)
latus rectum = 12 (3,-5) ! ! ! !
Problem 8 – Mathematics (Analytic Geometry) Find the length of the latus rectum of the curve 9x2 + 25y2 = 225. Solution: 9x2 + 25y2 = 225 x2 y2 25 + 9 = 1 a2 = 25 a=5 b2 = 9 b=3 2 b2 L= a 2 (9) L = 5 = 3.6
y a x V
F a=5
b=3
c
a
c F’ a=5
V’
Visit For more Pdf's Books Pdfbooksforum.com
Problem 9 – Mathematics (Analytic Geometry) What is the angle in degrees, between an asymptote of the hyperbola x2 - 4y2 - 2x - 63 = 0 and the x-axis? Solution: x2 - 2x + 1 - 4y2 - 63 = 1 (x - 2)2 - 4 (y - 0)2 = 64 (x - 2)2 (y - 0)2 =1 - 16 64 a2 = 64 a=8 b2 = 16 b=4 b tan θ = a 4 tan θ = 8 θ = 26.6˚
y
asymptote
θ
b
x
a
a
! ! ! !
Problem 10 – Mathematics (Analytic Geometry) Find the length of the latus rectum of the curve r Sin2 θ = Cos θ. Solution: r Sin2 θ = Cos θ r
(yr )
2
x =r
y2 x r =r y2 = x 4a = 1 (latus rectum)
y (r,θ)
r
y
θ
x
x
Visit For more Pdf's Books Pdfbooksforum.com
Problem 11 – Mathematics (Analytic Geometry) The vertices of a triangle have polar coordinates of (0, 0˚), (6, 30˚) and (9, 70˚). Find the area and perimeter of the triangle. B
Solution: 9 (6) Sin 40˚ Area = 2 Area = 17.36 sq.units (BC)2 = (9)2 + (6)2 - 2 (9)(6) Cos 40˚ BC = 5.85 Perimeter = 9 + 6 + 5.85 Perimeter = 20.85 units
(9, 70ß)
y 9
A (0, 0)
40ß 6 70ß 30ß
(6, 30ß) C
x
! ! ! !
Problem 12 – Mathematics (Analytic Geometry) The distance between the foci of an ellipse is 5. If its eccentricity is 0.5, what is the distance between the directrices? Solution: Directrix 2c = 5 y c = 2.5 e = 0.5 a b a c=ae V V’ x c c 2.5 = a (0.5) F F’ a=5 a d=e a a d=a/e d=a/e 5 d= 0.5 d = 10 Distance between directrices = 2 (10) = 20
Visit For more Pdf's Books Pdfbooksforum.com
Problem 13 – Mathematics (Analytic Geometry) Using polar coordinates, a point is at (7, 38˚). Find its rectangular coordinates. Solution: x = r Cos θ x = 7 Cos 38˚ x = 5.56 y = 7 Sin 38˚ y = 4.3 Rectangular coordinates (5.5, 4.3)
y (r,θ)
r
y
θ
x
! ! ! ! ! !
Problem 14 – Mathematics (Analytic Geometry) 2x4 Find the horizontal asymptote of the curve y = 4 x - 3x2 - 1 Solution: 2x4 y= 4 x - 3x2 - 1 2 y= 3 1 1- 2- 4 x x when x = α 2 y= 3 1 1- α α 2 y=1-0-0 y=2 y - 2 = 0 (horizontal asymptote)
x
Visit For more Pdf's Books Pdfbooksforum.com
Problem 15 – Mathematics (Analytic Geometry) The equation of a given conics is x2 + y2 = 25. Find the length of the sub-tangent at (-3, 4). Solution: y normal
tangent
4 θ θ
C D
AD = sub-tangent 3 4 AD = 4 AD = 5.33 ! ! ! ! ! !
3
x...
Similar Free PDFs

150 Geometry Problems With Solutions
- 23 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu