Analytic geometry formulas (maths) PDF

| Title | Analytic geometry formulas (maths) |
|---|---|
| Author | Shaira Erpe |
| Course | Bachelor of Science in Architecture |
| Institution | Polytechnic University of the Philippines |
| Pages | 4 |
| File Size | 134.7 KB |
| File Type | |
| Total Downloads | 58 |
| Total Views | 152 |
Summary
Analytic geometry...
Description
www.mathportal.org
Line segment
Line forms
A line segment P1P2 can be represented in parametric form by
Slope - intercept form:
y = mx + b
x = x1 + ( x 2 − x 1 )t
Two point form:
y − y1 =
y2 − y1 ( x − x1 ) x2 − x1
y = y1 + ( y 2 − y1 ) t 0≤ t ≤ 1
Point slope form:
Two line segments P1P2 and P3P4 intersect if any only if the numbers
y − y 1 = m ( x − x1 ) Intercept form
x2 − x1 x −x s= 3 1 x2 − x1 x3 − x 4
x y + = 1 ( a, b ≠ 0 ) a b Normal form:
x ⋅ cos σ + y sin σ = p
y 2 − y1 y 3 − y1 y2 − y1 y 3 − y4
x3 − x1 and
t=
y 3 − y1
x3 − x 4 y 3 − y 4 x2 − x1 y 2 − y1 x3 − x 4 y 3 − y 4
satisfy 0 ≤ s ≤ 1 and 0 ≤ t ≤ 1
Parametric form:
x = x 1 + t cosα y = y1 + t sin α
Point direction form:
x −x1 y − y1 = A B
Area
where (A,B) is the direction of the line andP1 ( x1, y1) lies on the line. General form:
A ⋅ x + B ⋅ y + C = 0 A ≠ 0 or B ≠ 0
The area of the triangle formed by the three lines:
A1x + B1 y + C1 = 0 A2 x + B2 y + C2 = 0 A3 x + B3 y + C3 = 0 is given by
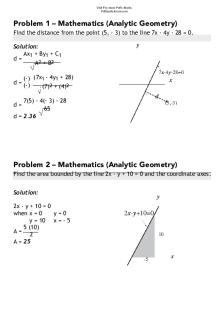
Distance The distance from Ax + By + C = 0 to P1 ( x1 , y1 ) is
d=
A ⋅ x1 + B ⋅ y1 + C
K= 2⋅
A2 + B 2
A1
B1 C 1
A2 A3
B2 C 2 B3 C 3
A1
B1
A2
B2
⋅
A2 A3
2
B 2 A3 B 3 ⋅ B3 A1 B1
The area of a triangle whose vertices are P1 ( x1 , y1 ) ,
Concurrent lines Three lines
A1x + B 1y + C 1 = 0 A2x + B 2y + C 2 = 0 A3x + B 3y + C 3 = 0 are concurrent if and only if:
A1
B1 C1
A2 B 2 C 2 = 0 A3
B3 C3
P2 ( x 2, y 2) and P3 ( x3 , y3 ) : x1 1 K = x2 2 x3
K=
y1 1 y2 1 y3 1
1 x 2 − x1 y 2 − y1 . 2 x3 − x1 y3 − y1
www.mathportal.org Centroid
The centroid of a triangle whose vertices are P1 (x1, y 1) ,
P2( x 2, y 2) and P3 ( x3 , y3 ) :
Equation of a circle
x + x + x y + y 2 + y3 ( x, y) = 1 2 3 , 1 3 3
In an x-y coordinate system, the circle with centre (a, b) and radius r is the set of all points (x, y) such that:
(x − a )2 + ( y − b )2
= r2
Circle is centred at the origin
Incenter
x2 + y 2 = r 2
The incenter of a triangle whose vertices areP1 (x1 , y1 ) ,
Parametric equations
x = a + rcos t y = b + r sin t
P2( x 2, y 2) and P3 ( x3 , y3 ) : ax + bx2 + cx3 ay1 + by2 + cy3 (x , y ) = 1 , a +b +c a +b +c
where t is a parametric variable. In polar coordinates the equation of a circle is:
where a is the length of P2 P3 , b is the length of P1P3 , and c is the length of P1P2.
r2 − 2 rro cos ( θ − ϕ ) + ro2 = a2
Area A = r 2π
Circumference
Circumcenter The
circumcenter
of a triangle whose vertices are
c = π ⋅ d = 2π ⋅ r
P1(x 1, y 1) , P2 ( x2 , y2 ) and P3 (x3 , y3 ) : x12 + y12 y1 1 x1 x12 + y12 1 2 2 y2 1 x2 x2 2 + y2 2 1 x2 + y2 x 2 +y 2 y 1 x x 2 +y 2 1 3 3 3 3 3 3 (x , y ) = , x1 y 1 1 x1 y 1 1 2 x2 y 2 1 2 x2 y 2 1 x3 y3 1 x3 y3 1
Theoremes: (Chord theorem) The chord theorem states that if two chords, CD and EF, intersect at G, then:
CD ⋅ DG = EG ⋅ FG (Tangent-secant theorem) If a tangent from an external point D meets the circle at C and a secant from the external point D meets the circle at G and E respectively, then 2
DC = DG ⋅ DE
Orthocenter The
orthocenter
of a triangle whose vertices are
P1(x 1, y 1) , P2 ( x2 , y 2 ) and P3 (x3 , y 3 ) : y1 x2 x3 + y 1 x + y2 y3 1 x + y 3 y1 y 2 x 3x1 + y y x x +y 1 x + y 1y 2 3 1 2 (x , y ) = , x1 y 1 1 x1 y 1 2 x2 y 2 2 x2 y 2 1 x3 y 3 1 x3 y 3 2 1 2 2 2 3
2 1 2 2 2 3
(Secant - secant theorem) If two secants, DG and DE, also cut the circle at H and F respectively, then:
DH ⋅ DG = DF ⋅ DE x1 1 x2 1 x3 1 1 1 1
(Tangent chord property) The angle between a tangent and chord is equal to the subtended angle on the opposite side of the chord.
www.mathportal.org
Eccentricity:
The Parabola The set of all points in the plane whose distances from a fixed point, called the focus, and a fixed line, called the directrix, are always equal.
y 2 = 2px
Area: K = π ⋅ a⋅ b
2
The Hyperbola
Tangent line 2
Tangent line in a pointD (x0 , y0 ) of a parabola y = 2 px
y 0y = p (x + x 0 ) Tangent line with a given slope (m)
p 2m
Tangent lines from a given point Take a fixed pointP (x 0, y 0) .The equations of the tangent lines are
y − y 0 = m 1 ( x − x 0 ) and y − y 0 = m 2 ( x − x 0 ) where m1 = m1 =
Foci:
if a < b => F1 (0, − b2 − a2 ) F2 (0, b2 − a2 )
Parametric equations of the parabola:
y = mx +
a 2 − b2 a
if a > b => F1 (− a 2 − b2 , 0) F2 ( a2 − b2 , 0)
The standard formula of a parabola:
x = 2 pt y = 2 pt
e=
y0 +
y0 2 − 2 px0 and 2 x0
y0 −
y0 2 − 2 px0 2 x0
The Ellipse The set of all points in the plane, the sum of whose distances from two fixed points, called the foci, is a constant.
The standard formula of a ellipse
x2 y 2 + =1 a2 b2 Parametric equations of the ellipse x = a cos t y = b sin t Tangent line in a point D( x0 , y0 ) of a ellipse:
x0 x y0 y + 2 =1 a2 b
The set of all points in the plane, the difference of whose distances from two fixed points, called the foci, remains constant.
The standard formula of a hyperbola: 2
2
x y − 2 =1 2 a b Parametric equations of the Hyperbola
a sin t b sin t y= cost x=
Tangent line in a point D (x 0 , y 0 ) of a hyperbola:
x0 x y 0 y − 2 =1 a2 b
Foci: if a > b => F1 (− a 2 + b2 , 0) F2 ( a2 + b2 , 0) if a < b => F1 (0, − b2 + a2 ) F2 (0, b2 + a2 )
Asymptotes:
b b x and y = − x a a a a if a < b => y = x and y = − x b b if a > b => y =
www.mathportal.org Plane forms Point direction form: x − x1 y − y1 z − z1 = = a b c where P1(x1,y1,z1) lies in the plane, and the direction (a,b,c) is normal to the plane.
General form:
Ax + By +Cz + D = 0 where direction (A,B,C) is normal to the plane.
Intercept form: x y z + + =1 a b c
Equation of a plane The equation of a plane through P1(x1,y1 ,z1) and parallel to directions (a1,b1,c1) and (a2,b2,c2) has equation
x − x1
y − y1
z − z1
a1
b1
c1
a2
b2
c2
The equation of a plane through P1(x1,y1,z1 ) and P2(x2,y2,z2), and parallel to direction (a,b,c), has equation
x − x1 x2 − x1
y − y1 y 2 − y1
a
b
z − z1 z 2 − z1 = 0 c
Distance
this plane passes through the points (a,0,0), (0,b,0), and (0,0,c).
x− x3
y − y3
x1 − x3 x2 − x3
y1 − y3 y2 − y3
The distance of P1(x1,y1,z1) from the plane Ax + By + Cz + D = 0 is
Ax1 + By1 + Cz 1
d=
Three point form z − z3 z1 − z3 = 0 z2 − z3
Normal form:
x cos α + y cos β + z cos γ = p Parametric form:
x = x1 + a1s + a 2t y = y 1 + b1s + b 2t z = z1 + c1 s + c2 t where the directions (a1,b1,c1) and (a2,b2,c2) are parallel to the plane.
Angle between two planes:
A2 + B 2 + C 2
Intersection The intersection of two planes
A1x + B1y + C 1z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0, is the line
x − x1 y − y1 z − z1 , = = a b c where
B1
C1
B2
C2
C1
A1
C2
A2
A1 A2
B1 B2
a=
b=
c=
The angle between two planes:
A1x + B1 y + C1z + D1 = 0 A2x + B 2 y + C 2 z + D2 = 0 is
arccos
=0
b x1 =
A1 A2 + B1B2 + C1C 2 A1 2 + B1 2 + C1 2 A2 2 + B 2 2 + C 2 2
The planes are parallel if and only if
A1 B1 C1 = = A2 B 2 C 2 The planes are perpendicular if and only if
A1A2 + B1B 2 +C 1C 2 = 0
y1 =
D1 D2
C1 D −c 1 C2 D2
B1 B2
a 2 + b2 + c 2 D A1 D1 C1 c 1 −c D2 A2 D2 C 2
a 2 +b 2 + c 2 D B1 D1 a 1 −b D2 B2 D2 z1 = 2 2 a +b +c2
A1 A2
If a = b = c = 0, then the planes are parallel....
Similar Free PDFs

Maths-Extension-1 Formulas
- 7 Pages

Solid geometry formulas
- 2 Pages

Tumws 20VDA-Formulas - Formulas
- 5 Pages

Formulas
- 2 Pages

125001-Formulas - formulas sheet
- 8 Pages

Formulas
- 6 Pages

Formulas
- 1 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu