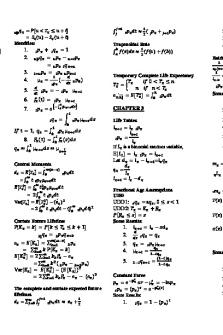342-0 - Introduction to Differential Geometry List of Formulas PDF

| Title | 342-0 - Introduction to Differential Geometry List of Formulas |
|---|---|
| Course | Introduction To Differential Geometry |
| Institution | Northwestern University |
| Pages | 2 |
| File Size | 62.9 KB |
| File Type | |
| Total Downloads | 103 |
| Total Views | 192 |
Summary
List of Formulas...
Description
342-0 - Introduction to Differential Geometry Northwestern University List of formulas which you will have to know for the final It is up to you to reconstruct the background of each formula, which is given without definitions, etc. This list is not complete, in the sense that it will not include some basics (like the equation of a circle, line, etc.) which you will also need to know. Also, these are just formulas, you will also need to know definitions of key concepts and problem-solving procedures. In other words, this list is just supposed to help you remember these formulas, it is not an exhaustive list of what you need to know for the final. • L(γ) = • s(t) =
∫
∫
b
∥γ ′ (t)∥dt
a
t
∥γ ′ (τ )∥dτ,
h = s−1 ,
γ˜ = γ ◦ h
a
• If ∥γ ′ (t)∥ = 1 then κ(t) = ∥γ ′′(t)∥ • T = • If ∥γ ′ (t)∥ = 1 then T = γ ′, • In R3 , T ′ = κN,
N ′ = −κT − τ B,
• In R2 , T ′ = κ ˜ N,
N ′ = −˜ κT,
κ ˜=
N =
γ ′′ , ∥γ ′′∥
B =T ×N
B′ = τ N 1 ∥γ ′ ∥3
det(γ ′ , γ ′′)
• A6 •
γ′ ∥γ ′ ∥
ℓ2 4π
Tp S = Im(dφq : R2 → R3 )
• Tp (f −1 (a)) = ∇f(p)⊥ , and N = • ∂1 =
∂φ , ∂u
∂2 =
∇f ∥∇f ∥
∂φ ∂v
• Ip (v) = ⟨v, v⟩p ,
E = ∥∂1 ∥2 , F = ⟨∂1 , ∂2 ⟩, G = ∥∂2 ∥2
• v = v1 ∂1 + v2 ∂2 ,
I(v) = Ev12 + 2F v1 v2 + Gv22
• IIp (v) = −⟨dNp (v), v⟩p , e = −⟨∂1 , dN (∂1 )⟩, f = −⟨∂1 , dN (∂2 )⟩ = −⟨∂2 , dN (∂1 )⟩, g = −⟨∂2 , dN (∂2 )⟩
1
• e=
⟨
N,
∂2φ ⟩ ∂u2
,f =
• v = v1 ∂1 + v2 ∂2 ,
⟨
∂2φ N, ∂u∂v
⟩ ∂2φ N, 2 ∂v
II(v) = k1 cos2 θ + k2 sin2 θ
v = cos θe1 + sin θe2 ,
H=
,g =
⟨
II(v) = ev 12 + 2f v1 v2 + gv22
• •
⟩
k1 + k2 , 2
eg − f 2 EG − F 2
K = k1 k2 =
• k12 = H ±
√
H2 − K
• ∥v∥ = 1, • •
DV (t) = Πγ(t) (V ′ (t)) = V ′ (t) − ⟨V ′ (t), N (t)⟩N (t) d ⟨V (t), W (t)⟩ = ⟨DV (t), W (t)⟩ + ⟨V (t), DW (t)⟩ dt
• • •
κn (v) = II(v )
Dγ ′ = γ ′′ − ⟨γ ′′, N ⟩N ∥γ ′ ∥ = 1, ∫
Dγ ′ (t) = κg (t)(N (t) × γ ′ (t)),
f dA =
R
∫ ∫
(f ◦ φ−1 )
∫
∑∫
ϕ−1 (R)
• R simple region,
KdA +
R
√
κ2 = κ2g + κn2
EG − F 2 dudv
ti+1
κg (s)ds +
ti
i
∑
αi = 2π
i
• χ = #F − #E + #V • R regular region,
∫
KdA +
R
∑∫ i
• S closed and bounded,
κg (s)ds +
Ci
∫
∑
αi = 2πχ(R)
i
KdA = 2πχ(S)
S
• χ(Σg ) = 2 − 2g • S1 #S2 , connected sum, χ(S1 #S2 ) = χ(S1 ) + χ(S2 ) − 2 • S minimal if H = 0
2...
Similar Free PDFs

Solid geometry formulas
- 2 Pages

Introduction to Law of Torts
- 14 Pages

Geometry Of Linear Programming
- 6 Pages
THE GEOMETRY OF UNCERTAINTY
- 80 Pages

Introduction to
- 22 Pages

Introduction to Ninth Edition Introduction to
- 1,073 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu