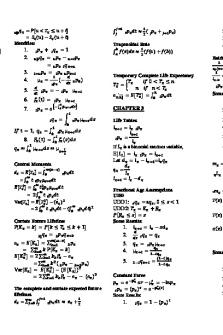Formula Sheet for Actuarial Mathematics - Exam MLC - (ASM 2014) PDF

| Title | Formula Sheet for Actuarial Mathematics - Exam MLC - (ASM 2014) |
|---|---|
| Author | Monica Revadulla |
| Pages | 34 |
| File Size | 345.8 KB |
| File Type | |
| Total Downloads | 564 |
| Total Views | 914 |
Summary
1 Lesson 1 - Probability Review Lesson 2 – Survival Distributions: Probability Functions 1.1 𝜇2 = 𝜇2′ − 𝜇 2 2.1 𝑆𝑥+𝑡 (𝑢) = 𝑆𝑥 (𝑡+𝑢) 𝑆𝑥 (𝑡) 1.2 𝜇3 = 𝜇3′ − 3𝜇2′ 𝜇 − 2𝜇 3 𝑆0 (𝑥+𝑡) 1.3 𝑉𝑎𝑟(𝑋) = 𝐸[𝑋 2 ] − 𝐸[𝑋]2 2.2 𝑆𝑥 (𝑡) = 𝑆0 (𝑥) 1.4 𝑉𝑎𝑟(𝑎𝑋 + 𝑏𝑌) = 𝑎2 𝑉𝑎𝑟(𝑋) + 2𝑎𝑏𝐶𝑜𝑣(𝑋, 𝑌) + 𝑏 2 𝑉𝑎𝑟(𝑌) 𝐹0 (𝑥+𝑡)−𝐹0 (𝑥) 2...
Description
1 Lesson 2 – Survival Distributions: Probability Functions
Lesson 1 - Probability Review 1.1 1.2 1.3 1.4 1.5 1.6
� = �′ − � � = �′ − �′ � − � = [ ]− [ ] + = ∑= = ̅ =
1.7
Bayes Theorem
1.8
Pr
1.9 1.10 1.11 1.12 1.13
|
|
=
=
∑=
=
Pr( | )Pr
2.1 2.2 +
�
=
,
�
+
2.4 2.5
Distribution Bernoulli Binomial Uniform Exponential
Mean
+
�
|
]+
Variance − −
�
=
|
+
=
+ −
=
−
=
|
+
−
−
+
+
Life Table Functions
Pr ( | )
[
=
2.3
=
Law of Total Probability (Discrete) Pr | = ∑ Pr Pr = ∑ Pr ∩ Law of Total Probability (Continuous) Pr = ∫ Pr | Conditional Mean Formula [ ] = [ [ | ]] Double Expectation Formula ]= [ [ [ | ]] Conditional Variance Formula =
+
=
| +
= =
+
= +
− +
=
+ −
+ +
+
[ | ]
−
Bernoulli Shortcut: If a random variable can only assume two values with prob and − , then = − −
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
and
Formula Summary of ASM 2014
2 Lesson 4 – Survival Distribution: Mortality . Go pe tz’ La � = >
Lesson 3 – Survival Distributions: Force of Mortality 3.1 �
3.2 �
3.3 �
3.4 �
3.5 3.6 3.7 3.8 3.9
+ +
+
+
=
�
=�
=−
=−
4.2
)
n( n
.
= exp − ∫ �
= exp − ∫ � = exp − ∫
+
+
+
�
� + = = < < + =
3.10 =∫ � + ′ If � + = � + + for If � + = �̂ + + �̅ + for
If � ′ + = �
+
for
4.4 |
�
+
=∫
+
�
′
=(
Makeha ’s La
n
= exp −
−
)
−
̂
. ̅
−
� = + > A is constant part of force of mortality *Adding A to � multiplies by e−μt
Weibull Distribution
+
′ = then then =
then
= exp −
n
−
� =
Constant Force of Mortality 4.5 � = � 4.6 = e−μt 4.7 (BLANK) Uniform Distribution 4.8 � =
4.9
4.10
=
−
=
−
= 4.11 | 4.12 (BLANK)
−
=
−
+
−
Beta Distribution � 4.13 � = 4.14
�
− −
− − −
�
�
= exp −
+
+
�−
�−
�−
�−
*The force of mortality is the sum of two uniform forces. is the product of uniform probabilities
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Formula Summary of ASM 2014
3 Lesson 5 – Survival Distributions: Moments Complete Future Lifetime ∞ 5.1 =∫ � +
5.2
5.3
5.4 5.5 5.6 5.7
∞
=∫ [ ]=
∫
∞
∞
= ∫ − = [min , ] � + + :̅̅̅| = ∫
:̅̅̅|
:̅̅̅| = ∫ [min ,
]=
∫
Special Mortality Laws − 5.8 = [ ]= = [ ]=
5.9
= [ ]= =
=
5.10 5.11
:̅̅̅|
:̅̅̅|
: ̅|
=
= =
=
�
�+ −
�
− − −
−
e−μ
(CFM) = ∑∞= e−μ = −e−μ = + .5 (UDD) (UDD) :̅̅̅| + .5 :̅̅̅| =
*For those surviving n years, min , = *For those not surviving n years, average future lifetime is , since future lifetime is uniform. * = [min , ] * = [ ] *If curtate, + :̅̅̅̅̅̅̅ + | , < , < , �Ƶ is the same as + :̅̅̅|
(Beta)
�+ − �
5.20 5.21 5.22
(UDD) (CFM) �+
(Beta) (UDD) (CFM)
+
+ .5
(UDD) +
(UDD)
−
(UDD)
Curtate Future Lifetime 5.12 = ∑∞= | − ∑ 5.13 + = ̅̅̅ : | = | ∞ 5.14 [ ] = ∑ = | ] = ∑ =− 5.15 [min , 5.16 = ∑∞= 5.17 :̅̅̅| = ∑ = − 5.18 [ ] = ∑∞= ]=∑ = 5.19 [min ,
|
−
+
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Formula Summary of ASM 2014
4 Lesson 6 – Survival Distributions: Percentiles and Recursions 6.1 = :̅̅̅| + + 6.2 = :̅̅̅| + + 6.3 = :̅̅̅̅̅̅̅ + + + − | + + = 6.4 = + + = 6.5 = + < ̅̅̅ ̅̅̅̅ ̅̅̅̅̅̅̅̅ : | : | + : − | ( + + :̅̅̅̅̅̅̅̅ < 6.6 :̅̅̅̅̅̅̅̅ − |+ − | ) :̅̅̅| = 6.7 + + + :̅̅̅̅̅̅̅ :̅̅̅| = + :̅̅̅̅̅̅̅ − | = − |
Lesson 7 – Survival Distributions: Fractional Ages Uniform Distribution of Deaths 7.1 + = − + + = − 7.2 = 7.3
7.4 7.5 �
+
=
−
� + = = + =
=
−
Function
−
+ + +
,
+
−
7.6 = + (UDD) Recall: 5.11 ( : ̅| = + .5 7.7 :̅̅̅| + .5 :̅̅̅| = Constant Force of Mortality 7.8 = −� 7.9 � = −ln 7.10 = −� = 7.11 + =
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
=
)
−
Table 7.1: Summary of Formulas for Fractional Ages UDD CFM − + − − − + − � + − ln − − ln � + + .5 :̅̅̅| :̅̅̅| + .5 + .5 : ̅| : ̅|
=
:̅̅̅|
+
+ :̅̅̅̅̅̅̅ − |
Formula Summary of ASM 2014
5 Lesson 8 – Survival Distributions: Select Mortality A man whose health was established 5 years ago will have better mortality than a randomly selected man. A life selected at age can never become a life selected at any higher age. [ ] will never become [ + ].
Lesson 10 – Insurance: Annual and 1/mthly – Moments + + = ∑∞= 10.1 [ ] = ∑∞= + | ∞ + + ∑ = 10.2 [ ] = ∑∞= = |
Table 10.1: Actuarial notation for standard types of insurance Name Present Value of RV Symbol + Whole life + < Term life ́ :̅̅̅| { < Deferred life | { + Deferred term | ́ :̅̅̅̅| { + < < + | + < Pure Endowment ́| :̅̅̅ { Endowment
= :̅̅̅| − ( = + = − = 10.5 | = + 10.6 − | = ́ :̅̅̅| = 10.7 = = ̅̅̅ ̅̅̅ ́: | + : | 10.8 =
10.3 10.4
+
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
+
=
+ +
−
{
+
:̅̅̅| )
− − +
<
+
+
:̅̅̅|
+
(CFM)
Formula Summary of ASM 2014
6 Table 10.2: EPV for insurance payable at EOY of death Type of Insurance CFM UDD ̅̅̅̅̅̅̅̅ − | Whole Life + ̅̅̅| n-year term − + �− ̅̅̅̅̅̅̅̅̅̅̅̅̅̅ n-year deferred life − + | + �− n-year pure endowment (� − + ) �−
Lesson 11 – Insurance: Continuous – Moments – Part I ∞ 11.1 = ̅ =∫ ∞ 11.2 ̅ = ∫ −� � + 11.3 11.4
11.5 11.6 11.7 11.8
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
̅ =
|
=
−
�+�
̅ = � �+� ̅ + = ̅ ̅ ́ :̅̅̅| = ̅ ( − |
̅
|
̅
́ :̅̅̅̅|
:̅̅̅|
=
̅ = ́| = :̅̅̅
= ̅ ( �
�+� −
̅
)=
−
−
̅ −
) =
�+�
( − + �+�
−( �
+
�
�+�
�+�
−
)=
)+
−
̅
�+�
� − �+�
−
�+�
�+�
−
−
�+�
Formula Summary of ASM 2014
7 Lesson 12 – Continuous – Moments – Part II
Lesson 13 – Insurance: Probabilities and Percentiles
Table 12.1 EPV for insurance payable at moment of death Type of Insurance CFM UDD � ̅̅̅̅̅̅̅̅̅ Whole Life − | �+ �− � ̅̅̅̅| n-year term − − �+� �+ �− � −� n-year deferred life − �+� ̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ − + | �+ �− − �+� −� n-year pure endowment (� − + ) �−
To calculate Pr for continuous , draw a graph of as a function of . Identify the parts of the graph that are below the horizontal line = , and the corresponding ’s. The al ulate the p o a ilit of being in the range of those ’s.
=∫
12.1 Gamma
=∫
12.2 If n=1,
=∫
12.3 If n=2, 12.4 ∫
12.5
�̅̅
− ̅̅̅|
Variance If = + =
=
∞
∞
̅̅̅̅| −
=
�
,
&
∞
+
−
−
−
−
+
=
!
=
=
+
−
For CFM, Pr
=
For discrete , identify .
� �
and then identify
+
corresponding to that
To calculate percentiles of continuous , draw a graph of as a function of . Identify where the lower parts of the graph are, and how they vary as a function of . For example, for whole life, higher leads to lower . For year deferred whole life, both < and higher lead to lower . Write an equation for the probability is less than in terms of mortality probabilities expressed in terms of . Set it equal to the desired percentile, and solve for or for for any . Then solve for (which is often )
are mutually exclusive, −
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Formula Summary of ASM 2014
8 Lesson 14 – Insurance: Recursive Formulas, Varying Insurance Recursive Formulas 14.1 = + = + 14.2 ̅̅̅ : | 14.3 = + ́ :̅̅̅| 14.4 | = −
+ |
+
15.2
+ :̅̅̅̅̅̅̅ − | +́ :̅̅̅̅̅̅̅ − |
15.3 15.4
Applying whole life recursive equation twice: = + + + � 14.5 � ̅ ̅ = �+�
15.5 +
14.6 Continuously whole life insurance (CFM) � = �+ ̅ ́ :̅̅̅| 14.7 � ̅ ̅ ́ :̅̅̅| + ̅ ̅ ́ :̅̅̅| = ̅ ̅ ́ :̅̅̅| ̅ + 14.8 � ́ :̅̅̅| + ́ :̅̅̅| = 14.9
� �
+ ́ :̅̅̅| = ∑
́ :̅̅̅|
=
́ :̅̅̅|
=
− |
̅
+
́ : ̅|
Lesson 15 – Insurance: Relationships ( Uniform Distribution of Deaths 15.1 ̅ =
́ :̅̅̅|
Recursive Formulas for Increasing and Decreasing Insurance 14.10 � ́ :̅̅̅| = ́ :̅̅̅| + � +́ :̅̅̅̅̅̅̅ − | � 14.11 � ́ :̅̅̅| = ́ : ̅| + ́ :̅̅̅̅̅̅̅ + − | 14.12 ́ :̅̅̅| = ́ : ̅| + +́ :̅̅̅̅̅̅̅ − | 14.13 = + ̅̅̅ ̅̅̅ ̅̅̅̅̅̅̅ ́: | ́: | ́: − |
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
15.6
̅
|
̅
�
́ :̅̅̅|
=
:̅̅̅|
=
̅ = =
̅ =
�
�
�
+
�
|
, ̅
,
́ :̅̅̅| ́ :̅̅̅|
+
́| :̅̅̅
Claims Acceleration Approach ̅ = + + ́ :̅̅̅| = ̅ = + | ̅ :̅̅̅| = + . ̅
= ̅ =
+ +
.
.
.
́ :̅̅̅| −
|
́ :̅̅̅|
+
́| :̅̅̅
Formula Summary of ASM 2014
9 Lesson 17 – Annuities: Discrete, Expectation
= − + − ̅̅̅| − + − + :̅̅̅| = ∑ = − ∑ = :̅̅̅| = ∞ ∑ = = | 17.15 Constant Force of Mortality + =
17.12 17.13 17.14
Annuities-Due Whole Life Annuities − 17.1 = 17.2 = −
Temporary Life Annuities −
:̅̅̅| = − :̅̅̅| =
17.3 17.4
:̅̅̅|
̅̅̅̅̅̅̅̅̅ + |
−
Whole life annuities − = +
− � +
Temporary life annuities = :̅̅̅| + :̅̅̅| + 17.16 = − ̅̅̅ ̅̅̅ ́: | : | :̅̅̅|
n-year certain-and-life annuity-due 17.7 17.8
̅̅̅|
=
̅̅̅̅̅̅̅̅̅ + |
−
=
− � +
−
Table 17.2: Actuarial notation for standard types of annuity-due Name Whole Life Temporary Life
Annual pmt at k min > min
17.9 17.10 17.11
PV , − , −
< nork > K x K x min , nort > T < nort > T < + > +
18.2 ̅ = 18.3 ̅ =
max , > max T, − ̅
18.5 ̅ = ∫
18.6 ̅ = 18.9
18.10
:̅̅̅|
:̅̅̅|
|̅
|̅
18.11 ̅
� �+�
−
=
:̅̅̅|
+
� �+�
=
� � − ̅ :̅̅̅| �
=
>
|̅
>
< > <
+
+
| ̅ :̅̅̅|
̅̅̅̅̅̅̅̅ :̅̅̅||
Whole Life and Temporary Life 19.1 19.2 19.3
− ̅
− ̅ �
−
:̅̅̅| − ̅ :̅̅̅| �
̅ =
= ̅ ( −
CFM: ̅ = ̅ + Relationships: ̅ = ̅ :̅̅̅| + ̅ ̅ ̅ ̅̅̅̅̅̅̅̅ :̅̅̅|| = ̅̅̅| + |
�+�
19.6 19.7
−
�+�
�+�
)=
̅
̅ =
− − �+� �+�
=
=
=
−
� ̅ −
+
̅
� ̅ ̅̅̅ − ̅ ̅̅̅ : | : | �
̅
(̅ − ̅ ) �
−
µ
+
− ̅
̅
:̅̅̅|
̅ :̅̅̅| − ̅ :̅̅̅| �
(
̅̅̅̅̅̅̅̅ + |)
̅ =
=
−
=
=
(
Other Annuities 19.13 [ ] = ∑∞= 19.14
−
µ
− (̅
:̅̅̅| )
̅ is 1 moment at twice FOI
19.12
�
:̅̅̅|
=
st
19.11
̅ ̅̅̅ − ̅ : |
∞
( ̅ ̅̅̅| ) =
19.10
=
[ ̅ ̅̅̅̅| ] = ∫
19.5
19.9
=
∞
[ ̅ ̅̅̅̅| ] = ∫ ̅ ̅̅̅|
19.4
Note: �
∞
= =
Symbol ̅ ̅ :̅̅̅|
19.8
�
− ̅ ∞ 18.4 ̅ = ∫ ̅ ̅|
18.7 ̅ 18.8 ̅
PV ̅ ̅̅̅| ̅ ̅̅̅| ̅̅̅̅| ̅ ̅̅̅| − ̅̅̅̅| ̅ ̅̅̅| − ̅̅̅̅| ̅̅̅̅̅̅̅̅̅ + | − ̅̅̅̅| ̅̅̅̅| ̅̅̅̅̅̅̅̅̅̅ + |
[
:̅̅̅| ]
=∑
:̅̅̅| −
−
=
−
:̅̅̅|
=
)
+
̅̅̅| − |
̅̅̅| − |
−
− +
−
̅̅̅|
=∑
− =
̅̅̅|
− |
+
−
̅̅̅|
+
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Formula Summary of ASM 2014
11 Lesson 20 – Annuities: Probabilities and Percentiles For the continuous whole life annuity PVRV Y, the relationship of as follows: = Pr − = Pr = Pr = Pr ln = Pr − = Pr
=
(−
to
21.2
= ̅ =
− ln − ln − ln −
ln
−
̅
To calculate a probability for an annuity, calculate the for which ̅ has the desired property. Then calculate the probability is in that range. , then
Some adjustments may be needed for discrete annuities or non-whole-life annuities, as discussed in the lesson. If forces of mortality and interest are constant, then the probability that the present value of payments on a continuous whole life annuity will be greater than its expected present value is Pr( ̅ ̅̅̅|
�
� � ) > ̅ )=( �+
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
=
Temporary
)
To calculate a percentile of an annuity, calculate the percentile of calculate ̅ ̅̅̅|
Lesson 21 – Annuities: Varying, Recursive Formulas Whole Life 21.1 = + +
:̅̅̅|
:̅̅̅|
:̅̅̅|
= = =
Deferred life = | = | |̅ =
̅
+
+
̅
+
+
+ +̅
: ̅|
+ :̅̅̅̅̅̅̅ − |+ :̅̅̅̅̅̅̅ − |+ ̅
+ :̅̅̅̅̅̅̅ − | + +
− |
− |
: ̅|
+
+
− |̅ +
n-year certain and life + ̅̅̅̅̅̅ ̅̅̅̅̅̅̅ − |+ :̅̅̅| = + ̅̅̅̅̅̅ ̅̅̅̅̅̅̅ − |+ :̅̅̅| = + ̅ ̅̅̅̅̅̅̅ = ̅ ̅| ̅̅̅̅̅̅̅ − |+ :̅̅̅|
Increasing/decreasing annuities � � + = + ̅� ̅ = �+μ ̅� ̅ :̅̅̅| + ̅ ̅ :̅̅̅| = ̅ :̅̅̅| �
:̅̅̅|
+
:̅̅̅|
=
+
̅̅̅̅̅̅̅̅̅̅̅̅̅̅ + :̅̅̅̅̅̅̅ − |
̅̅̅̅̅̅̅̅̅̅̅̅̅̅ + :̅̅̅̅̅̅̅ − |
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ + :̅̅̅̅̅̅̅ − |
:̅̅̅|
Formula Summary of ASM 2014
12
Lesson 24 – Premiums: Net Premiums for Discrete Insurances – Part I Future Loss = PV(Benefits) – PV(Gross Premiums) Equivalence Principle: EPV(Premiums) = EPV(Payments) E[FutureLoss]=0 Net Premium E[PVFB] = E[PVFP]
Lesson 22 – Annuities: 1/m-thly Payments − 22.1 ≈ − ≈
−
−
Uniform Distribution of Deaths (UDD) = 22.2 22.3 22.4
|
= = :̅̅̅|
Woolhouse’ Fo
22.8
|
22.9 ̅ ≈ 22.10
≈
≈
−
−
ln
22.6 µ ≈ − :̅̅̅|
|
ula
≈
22.7
−
:̅̅̅|
=
22.5
−
=
≈
:̅̅̅|
|
−
− −
−
+ −
−
−
−
+ ln
−
Similar Free PDFs

Mlc formula sheet (final)
- 5 Pages

Formula Sheet for Exam P
- 4 Pages

Formula Sheet for Exam 2
- 1 Pages
![Exam Formula Sheet [USED]](https://pdfedu.com/img/crop/172x258/og2vxxd15434.jpg)
Exam Formula Sheet [USED]
- 3 Pages

MAST10016 Exam formula sheet
- 2 Pages

Final Exam Formula Sheet
- 9 Pages

Exam Formula Sheet
- 10 Pages

Calculus Exam Formula Sheet
- 1 Pages

Exam 2 Formula Sheet
- 1 Pages

Final exam formula sheet
- 4 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu