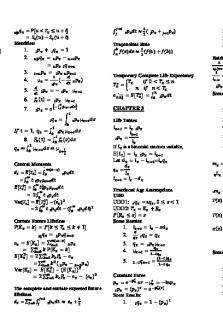Formula Sheet for Actuarial Mathematics PDF

| Title | Formula Sheet for Actuarial Mathematics |
|---|---|
| Author | Nallalingam Manoharan |
| Course | Financial accounting theory |
| Institution | Cambridge College |
| Pages | 34 |
| File Size | 568.8 KB |
| File Type | |
| Total Downloads | 24 |
| Total Views | 157 |
Summary
Formula Sheet for Actuarial Mathematics...
Description
1 Lesson 1 - Probability Review 1.1 1.2 1.3 1.4 1.5 1.6 1.7
1.8 1.9 1.10 1.11 1.12 1.13
𝜇2 = 𝜇′2 − 𝜇 2 𝜇3 = 𝜇′3 − 3𝜇2′ 𝜇 − 2𝜇 3 𝑉𝑎𝑟(𝑋) = 𝐸[𝑋 2 ] − 𝐸[𝑋]2 𝑉𝑎𝑟(𝑎𝑋 + 𝑏𝑌) = 𝑎2 𝑉𝑎𝑟(𝑋) + 2𝑎𝑏𝐶𝑜𝑣 (𝑋, 𝑌) + 𝑏 2 𝑉𝑎𝑟(𝑌) 𝑉𝑎𝑟(∑𝑛𝑖=1 𝑋𝑖) = 𝑛𝑉𝑎𝑟(𝑋) ∑𝑛 𝑋 𝑛𝑉𝑎𝑟(𝑋) 𝑉𝑎𝑟(𝑥) = 𝑉𝑎𝑟(𝑋 ) = 𝑉𝑎𝑟 ( 𝑖=1 𝑖) = 2 𝑛
Bayes Theorem Pr(𝐵 |𝐴)Pr(𝐴) Pr(𝐴|𝐵) =
𝑓𝑥 (𝑥|𝑦) =
𝑛
𝑛
Pr(𝐵)
𝑓𝑦( 𝑦|𝑥 )𝑓𝑥 (𝑥) 𝑓𝑦(𝑦)
Law of Total Probability (Discrete) Pr(𝐴) = ∑𝑖 Pr(𝐴 ∩ 𝐵𝑖 ) =∑ 𝑖 Pr(𝐵𝑖 )Pr(𝐴|𝐵𝑖 ) Law of Total Probability (Continuous) Pr(𝐴) = ∫ Pr(𝐴|𝑥) 𝑓(𝑥)𝑑𝑥 Conditional Mean Formula 𝐸𝑋 [𝑋] = 𝐸𝑌 [𝐸𝑋 [𝑋|𝑌]] Double Expectation Formula 𝐸𝑋 [𝑔(𝑋)] = 𝐸𝑌 [𝐸𝑋 [𝑔(𝑋 )|𝑌]] Conditional Variance Formula
Lesson 2 – Survival Distributions: Probability Functions
2.1 𝑆𝑥+𝑡 (𝑢) =
2.2 𝑆𝑥 (𝑡)
𝑆𝑥 (𝑡+𝑢 ) 𝑆𝑥 (𝑡) 𝑆0(𝑥+𝑡 ) = 𝑆 (𝑥) 0 𝐹0(𝑥+𝑡 )−𝐹0 (𝑥)
2.3 𝐹𝑥 (𝑡) =
2.4 2.5
𝑡|𝑢 𝑞𝑥
𝑡|𝑢 𝑞𝑥
1−𝐹0 (𝑥)
= 𝑡 𝑝𝑥 − 𝑡+𝑢 𝑝𝑥
= 𝑡+𝑢 𝑞𝑥 − 𝑡 𝑞𝑥
Life Table Functions 𝑡 𝑝𝑥
𝑡 𝑞𝑥
=
𝑡|𝑢 𝑞𝑥
=
𝑡+𝑢 𝑝𝑥
𝑙𝑥+𝑡
=
𝑙𝑥
𝑡 𝑑𝑥
𝑙𝑥
=
𝑢𝑑𝑥+𝑡
𝑙𝑥
𝑙𝑥 −𝑙𝑥+𝑡
=
𝑙𝑥
𝑙𝑥+𝑡−𝑙𝑥+𝑡+𝑢 𝑙𝑥
= 𝑡 𝑝𝑥 𝑢 𝑝𝑥+𝑡
𝑉𝑎𝑟𝑋 (𝑋) = 𝐸𝑌 [𝑉𝑎𝑟𝑋 (𝑋|𝑌)] + 𝑉𝑎𝑟𝑌 (𝐸𝑋 [𝑋|𝑌])
Distribution Bernoulli Binomial Uniform Exponential
Mean 𝑞 𝑚𝑞 𝑎+𝑏 2
𝜃
Variance 𝑞(1 − 𝑞) 𝑚𝑞(1 − 𝑞)
(𝑏−𝑎) 2 12
𝜃2
Bernoulli Shortcut: If a random variable can only assume two values 𝑎 and 𝑏 with prob 𝑞 and 1 − 𝑞 , then 𝑉𝑎𝑟(𝑋) = 𝑞 (1 − 𝑞 )(𝑏 − 𝑎)2
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Formula Summary of ASM 2014
2 3.1 𝜇𝑥+𝑡 =
𝑓𝑥 (𝑡 ) 𝑆𝑥 (𝑡)
Lesson 3 – Survival Distributions: Force of Mortality
3.2 𝜇𝑥+𝑡 =
𝑑 𝑞 𝑑𝑡 𝑡 𝑥
3.3 𝜇𝑥+𝑡 = −
3.4 𝜇𝑥+𝑡 = −
𝑡𝑝𝑥
𝑑 ln(𝑆𝑥 (𝑡 ))
4.2
𝑑𝑡 𝑑 ln( 𝑡𝑝𝑥 ) 𝑑𝑡
Lesson 4 – Survival Distribution: Mortality 4.1 Gompertz’ Law 𝜇𝑥 = 𝐵𝑐 𝑥 𝑐>1
3.5 𝑆𝑥 (𝑡) = exp(− ∫ 𝜇𝑥+𝑠 𝑑𝑠) 0 𝑡
3.7 𝑡 𝑝𝑥 = exp(− ∫𝑥 𝜇𝑠 𝑑𝑠) 3.8 𝑓𝑥 (𝑡) = 𝑆𝑥 (𝑡)𝜇𝑥+𝑡 = 𝑡 𝑝𝑥 𝜇𝑥+𝑡 𝑡+𝑢 3.9 𝑃(𝑡 < 𝑇𝑥 < 𝑡 + 𝑢) = 𝑡|𝑢 𝑞𝑥 = ∫𝑡 𝑠 𝑝𝑥 𝜇𝑥+𝑠 𝑑𝑠 𝑥+𝑡
𝑡 𝑞𝑥
= ∫0 𝑠 𝑝𝑥 𝜇𝑥+𝑠 𝑑𝑠 −𝑘𝑡 If 𝜇′𝑥+𝑠 = 𝜇𝑥+𝑠 + 𝑘 for 0 ≤ 𝑠 ≤ 𝑡 then 𝑡𝑝𝑥′ = 𝑝 . 𝑡 𝑥𝑒 If 𝜇𝑥+𝑠 = 𝜇 𝑥+𝑠 + 𝜇𝑥+𝑠 for 0 ≤ 𝑠 ≤ 𝑡 then 𝑡 𝑝𝑥 = 𝑡 𝑝𝑥 𝑡 𝑝𝑥 3.10
𝑡
If 𝜇′𝑥+𝑠 = 𝑘𝜇𝑥+𝑠 for 0 ≤ 𝑠 ≤ 𝑡 then 𝑡𝑝𝑥′ = ( 𝑡 𝑝𝑥)
= exp(−
𝑡 𝑝𝑥
= exp(−𝐴𝑡 −
𝐵𝑐 𝑥 (𝑐 𝑡−1) ln(𝑐)
𝑘
4.4
)
𝜇𝑥 = 𝐴 + 𝐵𝑐 𝑥 𝑐>1 A is constant part of force of mortality *Adding A to 𝜇 multiplies 𝑡 𝑝𝑥 by e−μt
4.3 Makeham’s Law
3.6 𝑡 𝑝𝑥 = exp(− ∫0 𝜇𝑥+𝑠 𝑑𝑠) 𝑡
𝑡 𝑝𝑥
𝐵𝑐 𝑥 (𝑐 𝑡−1) ln(𝑐)
)
𝜇𝑥 = 𝑘𝑥 𝑛 𝑘𝑥 (𝑛+1) ) 0𝑝𝑥 = exp(− 𝑛+1 Constant Force of Mortality 4.5 𝜇𝑥 = 𝜇 4.6 𝑡 𝑝𝑥 = e −μt 4.7 (BLANK) Weibull Distribution
Uniform Distribution 1 4.8 𝜇𝑥 = 0≤𝑥 ≤𝜔
4.9
𝑡 𝑝𝑥
𝜔−𝑥 𝜔−𝑥−𝑡
=
𝑡 𝑞𝑥
𝜔−𝑥 𝑡
0≤𝑡≤𝜔−𝑥
= 𝜔−𝑥 0 ≤ 𝑡 ≤ 𝜔 − 𝑥
4.11 𝑡|𝑢 𝑞𝑥 = 0≤𝑡+𝑢 ≤𝜔−𝑥 𝜔−𝑥 4.12 (BLANK)
4.10
𝑢
Beta Distribution 𝛼 4.13 𝜇𝑥 = 𝜔−𝑥 0 ≤ 𝑥 ≤ 𝜔 4.14
𝑡 𝑝𝑥
=(
𝜔−𝑥−𝑡 𝛼 𝜔−𝑥
) 0≤𝑡≤𝜔−𝑥
*The force of mortality is the sum of two uniform forces. 𝑡 𝑝𝑥 is the product of uniform probabilities
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Formula Summary of ASM 2014
3 Lesson 5 – Survival Distributions: Moments Complete Future Lifetime ∞ 5.1 𝑒𝑥 = ∫ 𝑡 𝑡 𝑝𝑥𝜇𝑥+𝑡 𝑑𝑡 0 ∞ 5.2 𝑒𝑥 = ∫0 𝑡 𝑝𝑥 𝑑𝑡
5.3 𝐸[𝑇𝑥2 ] = 2 ∫0 𝑡 𝑡 𝑝𝑥 𝑑𝑡 ∞ 5.4 𝑉𝑎𝑟(𝑇𝑥 ) = 2 ∫ 𝑡 𝑡 𝑝𝑥 𝑑𝑡 − 𝑒𝑥2 0 5.5 𝑒𝑥:𝑛| = 𝐸[min(𝑇𝑥 , 𝑛 )] 𝑛 𝑒𝑥:𝑛| = ∫ 𝑡 𝑡 𝑝𝑥 𝜇𝑥+𝑡 𝑑𝑡 + 𝑛 𝑛 𝑝𝑥 0 𝑛 5.6 𝑒𝑥:𝑛| = ∫ 𝑡 𝑝𝑥 𝑑𝑡 0 ∞
5.7 𝐸[min(𝑇𝑥 , 𝑛)2 ] = 2 ∫0 𝑡 𝑡 𝑝𝑥 𝑑𝑡 𝑛
5.20 𝑒𝑥 = ∑𝑘=1 e−μk = e (CFM) 1−e−μ 5.21 𝑒𝑥 = 𝑒𝑥 + 0.5 (UDD) 5.22 𝑒𝑥:𝑛| = 𝑒𝑥:𝑛| + 0.5 𝑛 𝑞𝑥 (UDD) ∞
−μ
*For those surviving n years, min(𝑇𝑥 , 𝑛) = 𝑛 𝑛 *For those not surviving n years, average future lifetime is 2 , since future lifetime is uniform. * 𝑒𝑥 = 𝐸[min(𝐾𝑥 , 𝑛)] * 𝑒𝑥 = 𝐸[𝑇𝑥 ] *If curtate,𝑒𝑥+𝑠:𝑎+𝑏| , 𝑏 < 1, 𝑠 < 1, 𝑎𝜖Ƶ is the same as 𝑒𝑥+𝑠:𝑎|
Special Mortality Laws 𝜔−𝑥 5.8 𝑒𝑥 = 𝐸[𝑇𝑥 ] = 𝛼+1 (Beta) 𝑒𝑥 = 𝐸 [𝑇𝑥 ] =
𝑒𝑥 = 𝐸 [𝑇𝑥 ] =
𝜔−𝑥 1
2
(UDD)
𝜇 𝛼(𝜔−𝑥) 2
(CFM)
5.9 𝑉𝑎𝑟(𝑇𝑥 ) = (𝛼+1)2(𝛼+2) (Beta) 𝑉𝑎𝑟(𝑇𝑥 ) =
𝑉𝑎𝑟(𝑇𝑥 ) =
(𝜔−𝑥 )2 1
𝜇2
12
(UDD)
(CFM)
5.10 𝑒𝑥:𝑛| = 𝑛 𝑝𝑥 (𝑛) + 𝑛 𝑞𝑥 ( ) (UDD) 2 𝑛
𝑒𝑥:𝑛| (𝑛) + = 𝜔−𝑥 5.11 𝑒𝑥:1| = 𝑝𝑥 + 0.5𝑞𝑥 (UDD) 𝜔−𝑥−𝑛
𝑛 𝑛 ( ) 𝜔−𝑥 2
(UDD)
Curtate Future Lifetime 5.12 𝑒𝑥 = ∑ ∞ 𝑘=0 𝑘 𝑘| 𝑞𝑥 𝑛−1 5.13 𝑒𝑥:𝑛| = ∑ 𝑘=0 𝑘 𝑘| 𝑞𝑥 + 𝑛 𝑛 𝑝𝑥 2 2 5.14 𝐸[𝐾𝑥 ] = ∑ ∞ 𝑘=0 𝑘 𝑘|𝑞𝑥 2 2 2 5.15 𝐸[min(𝐾𝑥 , 𝑛) ] = ∑ 𝑛−1 𝑘=0 𝑘 𝑘| 𝑞𝑥 + 𝑛 𝑛 𝑝𝑥 5.16 𝑒𝑥 = ∑ ∞ 𝑝 𝑘=1 𝑘 𝑥 𝑛 5.17 𝑒𝑥:𝑛| = ∑ 𝑘=1 𝑘 𝑝𝑥 2 5.18 𝐸[𝐾𝑥 ] = ∑ ∞ 𝑘=1(2𝑘 − 1) 𝑘 𝑝𝑥 5.19 𝐸[min(𝐾𝑥 , 𝑛)2 ] = ∑ 𝑛𝑘=1(2𝑘 − 1) 𝑘 𝑝𝑥
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Formula Summary of ASM 2014
4 Lesson 6 – Survival Distributions: Percentiles and Recursions 6.1 𝑒𝑥 = 𝑒 𝑥:𝑛| + 𝑛 𝑝𝑥 𝑒 𝑥+𝑛 6.2 𝑒𝑥 = 𝑒𝑥:𝑛| + 𝑛 𝑝𝑥 𝑒𝑥+𝑛 6.3 𝑒𝑥 = 𝑒𝑥:𝑛−1| + 𝑛 𝑝𝑥 (1 + 𝑒𝑥+𝑛 ) 6.4 𝑒𝑥 = 𝑝𝑥 + 𝑝𝑥 𝑒𝑥+1 = 𝑝𝑥 (1 + 𝑒𝑥+1 )𝑛 = 1 6.5 𝑒𝑥:𝑛| = 𝑒𝑥:𝑚| + 𝑚 𝑝𝑥𝑒𝑥+𝑚:𝑛−𝑚| 𝑚 < 𝑛 6.6 𝑒𝑥:𝑛| = 𝑒𝑥:𝑚−1| + 𝑚 𝑝𝑥(1 + 𝑒𝑥+𝑚:𝑛−𝑚| )𝑚 < 𝑛 = 𝑝𝑥 + 𝑝𝑥 𝑒𝑥+1:𝑛−1| = 𝑝𝑥 (1 + 𝑒𝑥+1:𝑛−1| ) 6.7 𝑒𝑥:𝑛|
Lesson 7 – Survival Distributions: Fractional Ages Uniform Distribution of Deaths 7.1 𝑙𝑥+𝑠 = (1 − 𝑠)𝑙𝑥 + 𝑠𝑙𝑥+1 = 𝑙𝑥 − 𝑠𝑑𝑥 7.2 𝑠 𝑞𝑥 = 𝑠𝑞𝑥 𝑠𝑞 𝑠𝑑𝑥 𝑙 7.3 𝑠 𝑞𝑥+𝑡 = 𝑥 = = 1 − ( 𝑥+𝑠+𝑡 ) , 0 ≤ 𝑠 + 𝑡 ≤ 1 1−𝑡𝑞𝑥
𝑙𝑥 −𝑡𝑑𝑥
7.4 𝑠 𝑝𝑥 𝜇𝑥+𝑠 = 𝑞𝑥 𝑞𝑥 𝑞 7.5 𝜇𝑥+𝑠 = 𝑥 = 1−𝑠𝑞 𝑠 𝑝𝑥
𝑙𝑥+𝑡
𝑥
7.6 𝑒𝑥 = 𝑒𝑥 + 2 (UDD) Recall: 5.11 (𝑒𝑥:1| = 𝑝𝑥 + 0.5𝑞𝑥 ) 7.7 𝑒𝑥:𝑛| = 𝑒𝑥:𝑛| + 0.5 𝑛 𝑞𝑥 1
Constant Force of Mortality 7.8 𝑝𝑥 = 𝑒 −𝜇 7.9 𝜇 = −ln(𝑝𝑥 ) 7.10 𝑠 𝑝𝑥 = 𝑒 −𝜇𝑠 = (𝑝𝑥 ) 𝑠 7.11 𝑠 𝑝𝑥+𝑡 = (𝑝𝑥 ) 𝑠 0 ≤ 𝑡 ≤ 1 − 𝑠
Table 7.1: Summary of Formulas for Fractional Ages UDD CFM 𝑙𝑥+𝑠 𝑙𝑥 − 𝑠𝑑𝑥 𝑙𝑥 𝑝𝑥𝑠 𝑠𝑞 1 − 𝑝𝑥𝑠 𝑥 𝑠 𝑞𝑥 1 − 𝑠𝑞 𝑝𝑥𝑠 𝑝 𝑥 𝑠 𝑥 𝑠𝑞 𝑥 1 − 𝑝𝑥𝑠 𝑠 𝑞𝑥+𝑡 1 − 𝑡𝑞𝑥 𝑞𝑥 − ln(𝑝𝑥 ) 𝜇𝑥+𝑠 1 − 𝑠𝑞𝑥 𝑞𝑥 −𝑝𝑥𝑠 ln(𝑝𝑥 ) 𝑠 𝑝𝑥 𝜇𝑥+𝑠 𝑒𝑥 𝑒𝑥 + 0.5 𝑒 𝑥:𝑛| 𝑒𝑥:𝑛| + 0.5 𝑛 𝑞𝑥 𝑒 𝑥:1| 𝑝𝑥 + 0.5𝑞𝑥
Function
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
𝑒 𝑥:𝑡| = 𝑒𝑥:𝑘| + 𝑘 𝑝𝑥 𝑒 𝑥+𝑘:𝑡−𝑘|
Formula Summary of ASM 2014
5 Lesson 8 – Survival Distributions: Select Mortality A man whose health was established 5 years ago will have better mortality than a randomly selected man. A life selected at age 𝑥 can never become a life selected at any higher age. [𝑥] will never become [𝑥 + 1].
Lesson 10 – Insurance: Annual and 1/mthly – Moments ∞ ∞ 10.1 𝐸[𝑍] = ∑𝑘=0 𝑏𝑘 𝑣 𝑘+1 𝑘|𝑞𝑥 = ∑ 𝑘=0 𝑏𝑘 𝑣 𝑘+1 𝑘𝑝𝑥 𝑞𝑥+𝑘 ∞ 2] 2 2 2(𝑘+1) 10.2 𝐸[𝑍 = ∑𝑘=0 𝑏𝑘 𝑣 2(𝑘+1) 𝑘| 𝑞𝑥 = ∑ ∞ 𝑘𝑝𝑥 𝑞𝑥+𝑘 𝑘=0 𝑏𝑘 𝑣
Table 10.1: Actuarial notation for standard types of insurance Name Present Value of RV Symbol Whole life 𝑣 𝐾𝑥 +1 𝐴𝑥 𝐴𝑥 :𝑛| Term life 𝑣 𝐾𝑥 +1 𝐾𝑥 < 𝑛 { 0𝐾𝑥 ≥ 𝑛 0𝐾𝑥 < 𝑛 Deferred life 𝑛| 𝐴𝑥 { 𝐾𝑥 +1 𝑣 𝐾𝑥 ≥ 𝑛 Deferred term 0𝐾𝑥 ≤ 𝑛 𝑛| 𝐴𝑥 :𝑚| {𝑣 𝐾𝑥 +1 𝑛 < 𝐾𝑥 < 𝑛 + 𝑚 𝐴 𝑛|𝑚 𝑥 0𝐾𝑥 ≥ 𝑛 + 𝑚 0𝐾𝑥 < 𝑛 Pure Endowment 𝐴𝑥:𝑛| { 𝑛 𝑣 𝐾𝑥 ≥ 𝑛 𝑣𝑡 𝑝 𝑣 𝐾𝑥 +1 𝐾𝑥 < 𝑛 𝑣 𝑛 𝐾𝑥 ≥ 𝑛 2 − (𝐴𝑥:𝑛| ) {
Endowment
10.3 𝑉𝑎𝑟(𝑍) = 2𝐴𝑥:𝑛| 10.4 2𝑖 = 2𝑖 + 𝑖 2 2 𝑑 = 2𝑑 − 𝑑 2 2 𝑣 = 𝑣2 10.5 𝑛|𝐴𝑥 = 𝑛 𝐸𝑥 𝐴𝑥+𝑛 10.6 𝐴𝑥 :𝑛| = 𝐴𝑥 − 𝑛|𝐴𝑥 = 𝐴𝑥 − 𝑛 𝐸𝑥 𝐴𝑥+𝑛 10.7 𝐴𝑥:𝑛| = 𝐴𝑥 :𝑛| + 𝑛 𝐸𝑥 = 𝐴 𝑥 − 𝑛 𝐸𝑥 𝐴𝑥+𝑛 + 𝑛 𝐸𝑥 𝑞 10.8 𝐴𝑋 = (𝐶𝐹𝑀) 𝑞+𝑖
𝑉𝑎𝑟(𝑍) = 𝑞+2𝑖+𝑖 2 − (
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
𝑞
𝑞
𝑞+𝑖
)
2
𝑡 𝑥
𝐴𝑥:𝑛|
(CFM)
Formula Summary of ASM 2014
6 Table 10.2: EPV for insurance payable at EOY of death Type of Insurance CFM UDD 𝑞 𝑎 Whole Life 𝜔−𝑥| 𝑞+𝑖 2 𝑞 𝑎 n-year term 𝑛| (1 − (𝑣𝑝)𝑛 ) 𝑞+𝑖 𝜔−𝑥 𝑞 𝑣 𝑛 𝑎𝜔−(𝑥+𝑛)| n-year deferred life (𝑣𝑝)𝑛 𝑞+𝑖 𝜔−𝑥 (𝑣𝑝)𝑛 n-year pure endowment 𝑣 𝑛 (𝜔 − (𝑥 + 𝑛)) 𝜔−𝑥
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Lesson 11 – Insurance: Continuous – Moments – Part I ∞ 11.1 𝐸(𝑍) = 𝐴𝑥 = ∫0 𝑣 𝑡 𝑓𝑥 (𝑡)𝑑𝑡 ∞ −𝛿𝑡 11.2 𝐴𝑥 = ∫0 𝑒 𝑡 𝑝𝑥 𝜇𝑥+𝑡 𝑑𝑡 2 11.3 𝑉𝑎𝑟(𝑍) = 𝐸(𝑍 2 ) − (𝐸(𝑍)) = 2 𝐴𝑥 − (𝐴𝑥 )2 𝜇 ( ) −𝑛 𝜇+𝛿 11.4 𝑛|𝐴𝑥 = 𝑒 𝐴𝑥 =
𝜇
𝜇+𝛿
𝜇+𝛿
(𝐶𝐹𝑀)
𝐴𝑥+𝑛 = 𝐴𝑥 (𝐶𝐹𝑀 ) 11.5 𝐴𝑥 :𝑛| = 𝐴𝑥 (1 − 𝑛 𝐸𝑥 ) =
11.6
𝑛| 𝐴𝑥 :𝑚|
11.8
𝑛| 𝐴𝑥
𝜇 (1 𝜇+𝛿
= 𝐴𝑥 ( 𝑛 𝐸𝑥 − 𝑚+𝑛 𝐸𝑥) =
− 𝑒 −𝑛(𝜇+𝛿) ) 𝜇𝑒 −𝑛(𝜇+𝛿) 𝜇+𝛿
𝜇 (1 − 𝑒 −𝑛(𝜇+𝛿) ) + 𝑒 −𝑛(𝜇+𝛿 ) 11.7 𝐴𝑥:𝑛| = 𝜇+𝛿
(1 − 𝑒 −𝑚(𝜇+𝛿) )
= 𝑛 𝐸𝑥 𝐴𝑥+𝑛 −𝑛(𝜇+𝛿 ) 𝐴𝑥:𝑛| = 𝑒
Formula Summary of ASM 2014
7 Lesson 12 – Continuous – Moments – Part II
Lesson 13 – Insurance: Probabilities and Percentiles
Table 12.1 EPV for insurance payable at moment of death Type of Insurance CFM UDD 𝜇 𝑎 Whole Life 𝜔−𝑥| 𝜇+𝛿 𝜔−𝑥 𝜇 𝑎𝑛| n-year term (1 − 𝑒 −𝑛(𝜇+𝛿) ) 𝜇+𝛿 𝜔−𝑥 𝜇 n-year deferred life 𝑒 −𝛿𝑛 𝑎𝜔−(𝑥+𝑛)| 𝑒 −𝑛(𝜇+𝛿) 𝜇+𝛿 𝜔−𝑥 n-year pure endowment 𝑒 −𝑛(𝜇+𝛿) 𝑒 −𝛿𝑛 (𝜔 − (𝑥 + 𝑛)) 12.1 12.2 12.3 12.4 12.5
∞ 𝑛! Gamma 𝐸𝑃𝑉 = ∫0 𝑡 𝑛 𝑒 −𝑐𝑡 𝑑𝑡 = 𝑐 𝑛 +1 ∞ 1 If n=1, 𝐸𝑃𝑉 = ∫0 𝑡𝑒 −𝑐𝑡 𝑑𝑡 = 2 𝑐 ∞ 2 If n=2, 𝐸𝑃𝑉 = ∫0 𝑡 2 𝑒 −𝑐𝑡 𝑑𝑡 = 3 𝑐 𝑢 1 ∫0 𝑡𝑒 −𝑐𝑡 𝑑𝑡 = 2 (1 − (1 + 𝑐𝑢)𝑒 −𝑐𝑢 ) 𝑐 𝑢 (𝑎𝑢| −𝑢𝑣 ) (𝐼𝑎 ) 𝑢| = 𝛿
𝜔−𝑥
To calculate Pr(𝑍 ≤ 𝑧) for continuous 𝑍, draw a graph of 𝑍 as a function of 𝑇𝑥 . Identify the parts of the graph that are below the horizontal line 𝑍 = 𝑧, and the corresponding 𝑡’s. Then calculate the probability of 𝑇𝑥 being in the range of those 𝑡’s. For CFM, Pr(𝑍 ≤ 𝑧) = 𝑧 𝛿
𝜇
For discrete 𝑍 , identify 𝑇𝑥 and then identify 𝐾𝑥 + 1 corresponding to that 𝑇𝑥 .
To calculate percentiles of continuous 𝑍 , draw a graph of 𝑍 as a function of 𝑇𝑥 . Identify where the lower parts of the graph are, and how they vary as a function of 𝑇. For example, for whole life, higher 𝑇 leads to lower 𝑍 . For 𝑛year deferred whole life, both 𝑇𝑥 < 𝑛 and higher 𝑇𝑥 lead to lower 𝑍 . Write an equation for the probability 𝑍 is less than 𝑧 in terms of mortality probabilities expressed in terms of 𝑡 . Set it equal to the desired percentile, and solve for 𝑡 or for 𝑒 𝑘𝑡 for any 𝑘. Then solve for 𝑧 (which is often 𝑣 𝑡 )
Variance If 𝑍3 = 𝑍1 + 𝑍2 , 𝑍1 &𝑍2 are mutually exclusive, 𝑉𝑎𝑟(𝑍3 ) = 𝑉𝑎𝑟(𝑍1 ) + 𝑉𝑎𝑟(𝑍2 ) − 2𝐸(𝑍1 )𝐸(𝑍2 )
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Formula Summary of ASM 2014
8 Lesson 14 – Insurance: Recursive Formulas, Varying Insurance Recursive Formulas 14.1 𝐴𝑥 = 𝑣𝑞𝑥 + 𝑣𝑝𝑥 𝐴𝑥+1 14.2 𝐴𝑥:𝑛| = 𝑣𝑞𝑥 + 𝑣𝑝𝑥 𝐴𝑥+1:𝑛−1| 14.3 𝐴𝑥 :𝑛| :𝑛−1| = 𝑣𝑞𝑥 + 𝑣𝑝𝑥 𝐴𝑥+1 14.4 𝑛| 𝐴𝑥 = 𝑣𝑝𝑥 𝑛−1|𝐴𝑥+1
Applying whole life recursive equation twice: 𝐴𝑥 = 𝑣𝑞𝑥 + 𝑣 2 𝑝𝑥 𝑞𝑥+1 + 𝑣 2 2𝑝𝑥 𝐴𝑥+2 )𝑥 = 𝜇 14.5 (𝐼𝐴 (𝜇+𝛿) 2
14.6 Continuously whole life insurance (CFM) 2𝜇 𝐸(𝑍 2 ) = (𝜇 + 2𝛿)3 )𝑥 :𝑛| 𝐴)𝑥 :𝑛| 14.7 (𝐼𝐴 + (𝐷 = 𝑛𝐴𝑥 :𝑛| (𝐷𝐴 ) 14.8 (𝐼𝐴)𝑥 :𝑛| + = (𝑛 + 1)𝐴𝑥 :𝑛| 𝑥 :𝑛| 14.9 (𝐼𝐴)𝑥 :𝑛| + (𝐷𝐴) 𝑥 :𝑛| = (𝑛 + 1)𝐴𝑥 :𝑛| 𝑛 (𝐼𝐴)𝑥 :𝑛| = ∑ 𝑘=1 𝑘 𝑘−1|𝐴𝑥 :1|
Recursive Formulas for Increasing and Decreasing Insurance 14.10 (𝐼𝐴)𝑥 :𝑛| = 𝐴 𝑥 :𝑛| + 𝑣𝑝𝑥 (𝐼𝐴)𝑥+1 :𝑛−1| 14.11 (𝐼𝐴)𝑥 :𝑛| = 𝐴𝑥 :1| + 𝑣𝑝𝑥 (𝐼𝐴𝐴)𝑥+1 :𝑛−1| 14.12 (𝐷𝐴)𝑥 :𝑛| :𝑛−1| = 𝑛𝐴𝑥 :1| + 𝑣𝑝𝑥 (𝐷𝐴)𝑥+1 14.13 (𝐷𝐴)𝑥 :𝑛| = 𝐴𝑥 :𝑛| + (𝐷𝐴)𝑥 :𝑛−1|
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Lesson 15 – Insurance: Relationships (𝐴𝑥 , 𝐴𝑥 , 𝐴𝑥 ) Uniform Distribution of Deaths 𝑖 15.1 𝐴𝑥 = ( ) 𝐴𝑥 𝑚
𝛿
𝑖 15.2 𝐴𝑥 :𝑛| = ( ) 𝐴𝑥 :𝑛| 𝛿
= ( 𝑖 ) 𝑛|𝐴𝑥 𝛿
𝑛|𝐴𝑥
𝑖 15.4 𝐴𝑥:𝑛| = ( ) 𝐴𝑥 :𝑛| + 𝐴𝑥:𝑛|
15.3
15.5 15.6
(𝑚) 𝐴𝑥 2
=
𝑖
𝛿
𝑖 (𝑚)
𝐴𝑥
2𝑖+𝑖 𝐴𝑥 = 2𝛿
2
𝐴𝑥
2
Claims Acceleration Approach
𝐴𝑥 = (1 + 𝑖)0.5 𝐴𝑥 0.5 𝐴𝑥 :𝑛| = (1 + 𝑖) 𝐴𝑥 :𝑛| 0.5 𝑛| 𝐴𝑥 = (1 + 𝑖) 𝑛| 𝐴𝑥 0.5 𝐴𝑥:𝑛| = (1 + 𝑖) 𝐴𝑥 :𝑛| + 𝐴𝑥:𝑛| 𝑚−1
𝐴𝑥 = (1 + 𝑖 ) 2𝑚 𝐴𝑥 2 𝐴𝑥 = (1 + 𝑖) 2𝐴𝑥 (𝑚)
Formula Summary of ASM 2014
9 = 𝑎 𝑥 − 𝑛 𝐸𝑥 𝑎 𝑥+𝑛 17.12 𝑎 𝑥:𝑛| 𝑛−1 17.13 𝑎 𝑥:𝑛| = ∑𝑘=1 𝑎 𝑘| 𝑘−1 𝑝𝑥 𝑞𝑥+𝑘−1 + 𝑎 𝑛| 𝑛−1 𝑝𝑥 𝑛−1 𝑘 ∑ = 17.14 𝑎 𝑥:𝑛| 𝑘=0 𝑣 𝑘𝑝𝑥 ∞ 𝑘 𝑛| 𝑎 𝑥 = ∑ 𝑘=𝑛 𝑣 𝑘𝑝𝑥 17.15 Constant Force of Mortality
Lesson 17 – Annuities: Discrete, Expectation Annuities-Due Whole Life Annuities 1−𝐴 17.1 𝑎 𝑥 = 𝑑 𝑥 17.2 𝐴𝑥 = 1 − 𝑑𝑎 𝑥
17.3 𝑎 𝑥:𝑛| =
𝑎 𝑥 =
𝑛| 𝑎 𝑥
1−𝐴𝑥:𝑛|
Temporary Life Annuities 𝑑
= 1 − 𝑑 𝑎 𝑥:𝑛| 17.4 𝐴𝑥:𝑛|
17.7 𝑎 𝑛| =
1−𝑣 𝑛
Whole life annuities 1 − 𝑖𝑎𝑥 𝐴𝑥 = 1+𝑖
𝑣 𝑛 −𝑣 𝐾𝑥 +1 𝑑
𝐾𝑥 ≤ 𝑛 − 1
𝐾𝑥 ≥ 𝑛
Temporary life annuities 1 = 𝑖𝑎𝑥:𝑛| + 𝐴𝑥:𝑛| + 𝑖𝐴𝑥 :𝑛| 17.16 𝐴𝑥 :𝑛| = 𝑣𝑎 𝑥:𝑛| − 𝑎𝑥:𝑛|
n-year certain-and-life annuity-due 𝑑
17.8 𝑎 𝐾𝑥 +1| =
1−𝑣 𝐾𝑥 +1 𝑑
𝐾𝑥 ≥ 𝑛
Table 17.2: Actuarial notation for standard types of annuity-due Name Whole Life Temporary Life Deferred Life Deferred Temporary Life Certainand-life
Annual pmt at k 10 ≤ 𝑘 ≤ 𝐾𝑥 10 ≤ 𝑘 ≤ min(𝐾𝑥 , 𝑛 − 1) 0𝑘 > min(𝐾𝑥 , 𝑛 − 1)
00 ≤ 𝑘 < n ork > Kx 1𝑛 ≤ 𝑘 ≤ K x 00 ≤ 𝑘 < n 1𝑛 ≤ 𝑘 < min(𝑛 + 𝑚, K x + 1) 0𝐾𝑥 ≥ min(𝑛 + 𝑚, Kx + 1) 10 ≤ 𝑘 < max(Kx + 1, 𝑛) 0𝑘 ≥ max(Kx + 1, 𝑛)
+ 𝑛| 𝑎 𝑥 𝑎 𝑥:𝑛| | = 𝑎 𝑛|
PV 𝑎 𝐾𝑥 +1| 𝑎 𝐾𝑥 < 𝑛 𝐾𝑥 +1| 𝑎 𝑛| 𝐾𝑥 ≥ 𝑛 0𝐾𝑥 < 𝑛 𝑎 − 𝑎 𝑛|𝐾𝑥 ≥ 𝑛 𝐾𝑥 +1| 0𝐾𝑥 < 𝑛 𝑎 − 𝑎 𝑛|𝑛 ≤ 𝐾𝑥 ≤ 𝑛 + 𝑚 𝐾𝑥 +1| 𝑎 − 𝑎 𝑛| 𝐾𝑥 ≥ 𝑛 + 𝑚 𝑛+𝑚| 𝑎 𝑛| 𝐾𝑥 < 𝑛 𝑎 𝐾𝑥 ≥ 𝑛 𝐾𝑥 +1|
𝑛| 𝑎 𝑥 = 𝑛 𝐸𝑥 𝑎 𝑥+𝑛 17.11 𝑎 𝑥 = 𝑎 𝑥:𝑛| + 𝑛|𝑎 𝑥
17.9
17.10
𝑞+𝑖
= 𝑛 𝐸𝑥 𝑎 𝑥
Annuities-immediate
n-year Deferred Whole Life Annuity 17.5 0𝐾𝑥 ≤ 𝑛 − 1 17.6 𝑎 𝐾𝑥 𝑛| = +1| − 𝑎
1+𝑖
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Symbol 𝑎 𝑥 𝑎 𝑥:𝑛| 𝑛| 𝑎 𝑥
𝑛| 𝑎 𝑥:𝑛|
𝑎𝑥:𝑛| |
Certain-and-life annuities 17.17 𝑎 𝑥 = 𝑎𝑥 + 1 17.18 𝑎 𝑥:𝑛| = 𝑎𝑥:𝑛−1| + 1
17.19 𝑎 𝑥:𝑛| = 𝑎𝑥:𝑛| + 1 − 𝑛 𝐸𝑥 17.20 𝑛| 𝑎 𝑥 = 𝑛| 𝑎𝑥 + 𝑛 𝐸𝑥
1/mthly annuities (17.1) 𝑎 𝑥
(𝑚)
(17.2) 𝐴𝑥
(𝑚)
17.21 𝑠𝑥:𝑛| =
=
(𝑚)
1−𝐴𝑥
𝑑(𝑚)
= 1 − 𝑑(𝑚) 𝑎 𝑥
𝑎 𝑥:𝑛|
(𝑚)
𝑛 𝐸𝑥
Official Definition: 𝑎 𝑥 = ∑∞ 𝑛=1 𝑎 𝑛 ( 𝑛−1𝑞𝑥 ) Alternative ∞ 𝑎 𝑥 = ∑𝑛=0 𝑣 𝑛 𝑛 𝑝𝑥
Formula Summary of ASM 2014
10 18.1 𝑎 𝑇𝑥| =
Lesson 19 – Variance
Lesson 18 – Annuities: Continuous, Expectation Name Whole Life Temporary Life Deferred Life Deferred Temporary Life Certainand-life
1−𝑣 𝑇𝑥 𝛿
Annual pmt at k 1𝑡 ≤ 𝑇 1𝑡 ≤ min(𝑇, 𝑛) 0𝑡 > min(𝑇, 𝑛)
PV 𝑎 𝑇| 𝑎 𝑇| 𝑇 ≤ 𝑛 𝑎𝑛| 𝑇 > 𝑛 0𝑇 ≤ 𝑛 𝑎 𝑇| 𝑛| − 𝑎 𝑇 > 𝑛 0𝑇 ≤ 𝑛 𝑎 𝑇| 𝑛| − 𝑎 𝑛 < 𝑇 ≤ 𝑛 + 𝑚 𝑛| 𝑎 − 𝑎 𝑇 > 𝑛 + 𝑚 𝑛+𝑚| 𝑎 𝑛| 𝑇 < 𝑛 𝑎 𝑇 ≥ 𝑛 𝐾𝑥 +1|
0𝑡 ≤ nort > T 1𝑛 < 𝑡 ≤ 𝑇 0𝑡 ≤ nort > T 1𝑛 < 𝑡 ≤ 𝑛 + 𝑚𝑜𝑟𝑡 ≤ 𝑇 0𝑇 > 𝑛 + 𝑚 1𝑡 ≤ max(𝑇, 𝑛) 0𝑡 > max(T, 𝑛)
18.2 𝑎𝑥 = 𝛿 𝑥 18.3 𝐴𝑥 = 1 − 𝛿𝑎𝑥 ∞ 18.4 𝑎𝑥 = ∫0 𝑎𝑡| 𝑡 𝑝𝑥 𝜇𝑥+𝑡 𝑑𝑡 ∞ 18.5 𝑎𝑥 = ∫0 𝑣𝑡 𝑡 𝑝𝑥 𝑑𝑡 1−𝐴
18.6 𝑎𝑥 =
𝜇 1− 𝜇+𝛿
=
𝛿 𝜇+𝛿
𝛿 𝛿 1−𝐴𝑥:𝑛|
18.7 𝑎𝑥:𝑛| = 𝛿 18.8 𝐴𝑥:𝑛| 𝑥:𝑛| = 1 − 𝛿𝑎 18.9
18.10
𝑥 𝑛| 𝑎
=
𝑥 𝑛| 𝑎
1−𝐴𝑥 𝛿
−
=
𝛿
= 𝑛 𝐸𝑥 𝑎𝑥 =
1
=
∞
19.2 𝐸[𝑎2𝑇 ] = ∫0 ( 𝑥|
𝑥 𝑛| 𝑎
19.3 𝑉𝑎𝑟(𝑎 𝑇𝑥 | ) =
𝑎𝑥:𝑛| |
− 𝑎 19.6 𝑉𝑎𝑟(𝑌) = 𝑥 𝛿 𝑥 − (𝑎𝑥 )2 2 = 1 − (2𝛿) 𝑎𝑥:𝑛| 19.7 2𝐴𝑥:𝑛|
𝑥:𝑛| 𝑛| 𝑎
𝜇+𝛿
𝛿
(𝐶𝐹𝑀)
1−𝑒 −𝑛(𝜇+𝛿) 𝜇+𝛿
𝛿2
2 2 𝐴 𝑥:𝑛| −(𝐴 )
𝑥:𝑛| 19.4 𝑉𝑎𝑟(𝑌) = 𝛿2 2 19.5 𝐴𝑥 = 1 − (2𝛿) 2 𝑎𝑥
2(𝑎
19.8 𝑉𝑎𝑟(𝑌) =
2
)
2 2(𝑎𝑥:𝑛| − 𝑎 ) 𝑥:𝑛|
− (𝑎𝑥:𝑛|) Note: 𝑎𝑥 is 1st moment at twice FOI 2
𝛿
2
2
𝐴𝑥−(𝐴𝑥 )2 𝑑2
𝐴𝑥:𝑛| −(𝐴𝑥:𝑛| )
2
19.10 𝑉𝑎𝑟(𝑌) = 𝑑2 19.11 2𝐴𝑥 = 1 − 2𝑑 2𝑎 𝑥 = 1 − (2𝑑 − 𝑑2 ) 2𝑎 𝑥
(𝐶𝐹𝑀)
𝑒 −𝑛(𝜇+𝛿)
2
) 𝑡 𝑝𝑥 µ𝑥+𝑡 𝑑𝑡 𝛿 2 ( )2 𝐴 𝑥− 𝐴 𝑥
∞ 1−𝑣𝑡
19.9 𝑉𝑎𝑟(𝑎 𝐾𝑥 +1| ) =
19.12 𝑉𝑎𝑟(𝑌) =
𝐴𝑥:𝑛| −𝐴𝑥
18.11 𝑎𝑥:𝑛| 𝑥 (1 − 𝑛 𝐸𝑥 ) = = 𝑎
CFM: 𝑎𝑥 = 𝑎𝑥+𝑛 Relationships: 𝑎𝑥 = 𝑎𝑥:𝑛| 𝑥+𝑛 + 𝑛 𝐸𝑥 𝑎
2 ] = ∫0 𝑎𝑇| 19.1 𝐸[𝑎2𝑇 𝑡 𝑝𝑥 µ𝑥+𝑡 𝑑𝑡 𝑥|
Whole Life and Temporary Life
2
𝜇+𝛿
1−𝐴𝑥:𝑛|
Symbol 𝑎𝑥 𝑎𝑥:𝑛|
(𝐶𝐹𝑀)
2(𝑎 𝑥 − 2𝑎 𝑥 ) + 2𝑎 𝑥 𝑑
Other Annuities 2 19.13 𝐸[𝑌𝑥 2 ] = ∑ ∞ 𝑘=1 𝑎 𝑘|
𝑘−1|𝑞𝑥
2 2 ] = ∑𝑛𝑘=1 𝑎 𝑘| 19.14 𝐸[𝑌𝑥:𝑛|
𝑘−1|𝑞𝑥
− (𝑎 𝑥 )2
2 + 𝑛 𝑝𝑥𝑎 𝑛|2 = ∑𝑛−1 𝑘| 𝑘=1 𝑎
𝑘−1|𝑞𝑥
+ 𝑛−1 𝑝𝑥𝑎 𝑛|2
𝑛| 𝑥 𝑎𝑥:𝑛| + 𝑛|𝑎 | = 𝑎
Monica E. Revadulla EXAM MLC – Models for Life Contingencies
Formula Summary of ASM 2014
11 Lesson 20 – Annuities: Probabilities and Percentiles
For the continuous whole life annuity PVRV Y, the relationship of 𝐹𝑌 (𝑦)to 𝐹𝑥 (𝑡) as follows: 𝐹𝑌 (𝑦) = Pr(𝑌 ≤ 𝑦) 1 − 𝑣 𝑇𝑥 = Pr( ≤ 𝑦) 𝛿 = Pr(𝑣 𝑇𝑥 ≥ 1 − 𝛿𝑦) = Pr(𝑇𝑥 ln 𝑣 ≥ ln(1 − 𝛿𝑦)) = Pr(−𝑇𝑥 𝛿 ≥ ln(1 − 𝛿𝑦)) ln(1 − 𝛿𝑦) = Pr (𝑇𝑥 ≤ ) 𝛿 ln(1 − 𝛿𝑦) = 𝐹𝑥 (− ( )) 𝛿
To calculate a probability for an annuity, calculate the 𝑡 for which 𝑎𝑡 has the desired property. Then calculate the probability 𝑡 is in that range.
To calculate a percentile of an annuity, calculate the percentile of 𝑇𝑥 , then calculate 𝑎𝑇𝑥 |
Some adjustments may be needed for discrete annuities or non-whole-life annuities, as discussed in the lesson. If forces of mortality and interest are constant, then the probability that the present value of payments on a continuous whole life annuity will be greater than its expected present value is Pr(𝑎 𝑥 ) = ( 𝑇𝑥 | > 𝑎
𝜇
𝜇 𝛿 ) 𝜇+𝛿
Monica E. Revadu...
Similar Free PDFs

Formula Sheet for Chemistry
- 1 Pages

Formula Sheet for final
- 4 Pages

Formula Sheet for ACCT2211
- 1 Pages

Formula Sheet - for exams
- 1 Pages

Formula Sheet for Geometry
- 2 Pages

Formula Sheet for Accounting
- 3 Pages

Lecture Notes on Actuarial Mathematics
- 320 Pages

Formula Sheet for Exam P
- 4 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu