Tutorial Gretl PDF

| Title | Tutorial Gretl |
|---|---|
| Course | Econometria I |
| Institution | Universitat Autònoma de Barcelona |
| Pages | 14 |
| File Size | 932.2 KB |
| File Type | |
| Total Downloads | 72 |
| Total Views | 138 |
Summary
Apuntes de la aplicación de GRETL...
Description
TUTORIAL GRETL EJECUTAR EL PROGRAMA · · ·
Buscar en Google “descargar Gretl”. Descargamos para Windows y aceptamos todo. Los datos que utilizan los manuales son: Introductory Econometrics y Introduction to Econometrics (aquí hay dos paquetes, se descargan los dos).
UTILIZACIÓN DEL PROGRAMA · ·
Usar FILE: Cargar los datos que nosotros queramos, por ejemplo, si hacemos una encuesta. Si le damos a Sample File, cargamos unos datos ya predeterminados de Gretl. Seleccionamos Sample File, y aparecen tres pestañas, Gretl, Greene y Ramanathan, que son tres manuales ya hechos. En el caso de haber descargado los dos paquetes, también nos aparecerán aquí.
EJEMPLO: Greene7_8 ·
Después de descargar los paquetes del punto 3, seleccionamos “greene7_8”. Y se nos abrirá otra ventana con todas las variables.
·
Si hacemos doble click a una variable (Pg) se nos vuelve abrir una ventana, con todos los años y el precio de cada año correspondiente. Si le damos al emoticono de arriba a la derecha “ ” se nos hará un gráfico con todos los datos. Son datos de serie temporales, porque por cada año hay una variable.
1
· ·
Los valores 0 y 1 significan SI o NO. “Tools / Herramientas ” y le damos a “Statistical table / Tablas estadísticas”, donde nos salen todas las distribuciones.
EJEMPLO SALARIO. Creación de un modelo de regresión. ·
·
·
Wage1. Estudiar salarios en un mercado. Por ejemplo, queremos saber el cambio de salario si estudiamos un año más. Con estas dadas podemos hacer un modelo de regresión, siendo beta 1 y beta 0 … FALTA Para poder estimarlo, en la barra de abajo hay una beta, clicamos. Nos sale una beta, y solo tenemos que seleccionar las variables que queremos como dependientes. SIEMPRE SE DEJA CONST EN REGRESSORS. ¿Cuándo es indiferente quitarlo? La estimación de beta gorro es cero cuando la Mitjana de X e Y sean 0. Le damos al okey y nos saldrá una tabla. El valor de los parámetros nos aparece en la columna “coefficient”. Beta gorro 1 es una variable aleatoria. Si tuviera otra muestra con otra gente, beta gorro 1 será diferente. El 0,541359 significa: por un año más de educación el salario augmenta 0,541359€. Si estudiamos 10 años más, cobraremos 5€ más por hora.
¿QUÉ SIGNIFICAN LOS VALORES QUE ENCONTRAMOS EN LA TABLA DE REGRESIÓN? · ·
Sum Squared Resid = Suma de cuadrados elevados Suma de los cuadrados totales = SEC / STC R2 = 1 − R2 = 1 −
SRC ST C ∑ u2i ST C
− R2 + 1 = SRC ST C
SRC ST C
= 1 − R2
ST C =
SRC 2 1−R
·
Data: para cambiar los datos View: dentro de aquí hay una opción para hacer una gráfica “graph specified vars”. Para que sea de dispersión se llama X-Y scatter. Tengo tantas barritas verticales rojas porque no puedo tener 5,4 años de educación, serán números enteros. Cada rayita dentro de la barra roja son las personas que tienen esos años. La raya azul es la recta de regresión poblacional. Variable: si le damos a summary statistics nos dirá la mitjana, mediana, mínimo, máximo, etc.
1.
FORMAS FUNCIONALES
· ·
Hasta ahora hemos visto relaciones lineales entre variables, por ejemplo, salario y educación. Sin embargo, en muchos trabajos econométricos, encontraremos otros tipos de relaciones, como casos en que una o las dos variables aparecen en forma logarítmica. En este apartado, estudiaremos la interpretación de los parámetros en el caso en que una o las dos variables del modelo de regresión sean especificadas en logaritmos.
CASOS
2
CASO 0
MODELO Nivel-nivel
DEPENDIEN. y
INDEP. x
INTERPRETACIÓN β1 ∆y = β 1 * ∆x
1 2 3
Log-nivel Log-log Nivel-log
Log (y) Log (y) y
%∆y = (100 − β 1 ) * ∆x %∆y = β 1 %∆x
x Log (x) Log (x)
∆y =
( ) %∆x β1 100
MODELO REGRESIÓN y = β0 + β1 x + u
Log (y) = β0 + β 1 x + u Log (y) = β0 + β 1 log(x) + u y = β 0 + β 1 log(x) + u
CASO 0: NIVEL - NIVEL Modelo de regresión y = β0 + β1 x + u Interpretación ∆y = β 1 * ∆x Ejemplo: Salario = -0.9 + 0.54 educación 0.54€/h de más por cada año de educación. -
∆Educ = 20 ∆y = β 1 * ∆x = 0.54 * (20) = 10.8 € Estudiar 20 años hace que aumente el salario en 10.8€
CASO 1: LOG - NIVEL Modelo de regresión Log (y) = β0 + β 1 x + u Interpretación %∆y = (100 − β 1 ) * ∆x Ejemplo: log (salario) = 0.584 + 0.083 educación 0.083€/h más por cada año de educación -
∆ Educ = 1 %∆y = (100 − β 1 ) * ∆x = (100*0.083) * (1) = 8.3% Estudiar 1 año más hace que aumente el salario un 8.3% ∆ Educ = 10 %∆y = (100 − β 1 ) * ∆x = (100*0.083) * (10) = 83% Estudiar 10 años más hace que aumente el salario un 83%
CAS0 2: LOG-LOG Modelo de regresión Log (y) = β0 + β 1 log(x) + u Interpretación %∆y = β 1 %∆x En este caso β 1 tiene la interpretación de elasticidad y expresa cuánto varia en términos porcentuales y si x aumenta en un 1%. Ejemplo: log (salario) = 4.82 + 0.25 log (ventas) 0.25% €/h más por cada 1% de aumento de ventas elasticidad -
∆ Ventas = 1% %∆y = β 1 %∆x = 0.25 * 1% = 0.25 Si las ventas aumentan un 1%, el salario aumentará un 0.25%
CASO 3: NIVEL-LOG Modelo de regresión y = β 0 + β 1 log(x) + u
3
Interpretación ∆y =
( ) %∆x β1 100
Ejemplo: Salario = 898.93 + 262.9 log (ventas) aumenta 2.629€ 2.
= 2 .629 por cada 1% de aumento, el salario ( 262.9 100 )
β1 ∆ Ventas = 1% ∆y = ( 100 ) %∆x = (262.9/100) * 1 = 2.629 Si las ventas aumentan 1%, el salario aumentará 2.629€
INTERPRETACIÓN GRETEL
Cada vez que cambiamos de caso, es decir utilizamos otra muestra debemos borrar archivo de datos. También para crear un modelo de regresión debemos tener en cuenta que variables poner en la variable dependiente - sería la constante - y que variables poner en regresores, que son aquellas variables que pueden o no explicar la variable dependiente. CASO 1. GRILICHES.GDT Modelo 1 1. 2. 3.
En los regresores elegimos poner Const y S. En la variable dependiente ponemos lw logaritmo de los salarios. Si incrementas los años de estudio 1 año, β 1 lo multiplicamos por 100 al ser un logaritmo y ese será el efecto de y. ∆X1 de 1 unidad→ β1 * 100
4.
Observamos en la tabla
Observamos la S, si incrementamos 1 año de estudio el salario (lw) aumentará 0.09 (9%).
5. 6.
Interpretación del pvalor. Es muy cercano a 0. tiene ***, por tanto, esto nos dice que será significativo en un nivel de confianza del 1%. Si p-valor < α rechazamos la Ho: β 1 = 0. R-cuadrado nos dice cuanto de la variable dependiente (salario) es explicada por este modelo, y lo que no se explica en este modelo se encuentra en el error ( U i ).
Modelo 2 1. 2.
Regresores S, Iq, Expr. Variable dependiente Lw.
4
3. 4. 5. 6.
R – cuadrado se ha incrementado, ya que, al incluir más variables explicamos más de la variable dependiente. Interpretación del regresor Iq: ∆X1 tendremos un salario de 0,4% más. La F te mira si la Ho: β 1 = β 2 = β 3 =⋯ = 0 son igual al mismo tiempo o no. El estadístico T te hace coeficiente por coeficiente, mientras que, F te los hace todo junto.
Modelo 3 -
Regresores: Iq Dependiente: Lw
Hay un coeficiente de un 0,5%, en el ejemplo anterior había un coeficiente más pequeño, pero tenías en cuenta más variables, eso es debido a que, habíamos incluido variables omitidas, es decir, variables que no estaban relacionadas con el salario. Modelo 4 1. 2.
Dependiente: Lw Regresores: Iq, S, Age, Expr, Smsa, Mrt, Rns.
Si incluimos más variables, vemos que Expr (experiencia de trabajo) no es importante para el salario, ya que, su coeficiente es negativo, lo que quiere decir que a menor experiencia más salario, cosa que no tiene mucho sentido.
5
La R-cuadrado ahora es del casi 100%, eso quiere decir que casi todos los factores que condicionan al salario se encuentran en este modelo. El coeficiente de los que residen en el sur de Estados Unidos (Rns), nos dice que aquellas personas que residan al sur tendrán un salario inferior. El coeficiente de las personas que están casadas (Mrt), nos dice que aquellas personas que estén casadas tienen un salario más elevado de 9%. Al ser logaritmo, se debe multiplicar por 100. Gretl te permite poner directamente para que salgan los coeficientes multiplicados por 100. Para eso debemos: -
Nos ponemos encima de Lw, botón derecho y le damos a definir nueva variable.
-
Definimos la variable lw100 para que salga directamente por 100.
Resultado con la variable dependiente lw100:
CASO 2: ENGEL.GDT Modelo 1
6
-
Dependiente. Foodexp Regresor. Income
-
Aprietas el botón derecho en las dos variables, y le das a ‘’añadir logaritmos’’, entonces cambias la interpretación.
-
Al hacerlo, nos cambia la interpretación.
Si voy incrementando cada año el salario en un 1% aumentará el consumo familiar en un 0,85%.
En las familias más pobres, el efecto en el consumo de un aumento de salario es muy grande, ya que, al obtener más dinero mensualmente lo dedicarán casi todo ese incremento en el consumo familiar, puesto que, lo que más necesitan son alimentos y cosas del hogar. CASO 3. RAC3D -
Illnes. Tener enfermedades en las últimas dos semanas. Incomes. Salario en un año. Chcond 2. Condición crónica que te limita en tu actividad.
Modelo 1 -
Dependiente. Illness Regresores. Prescrib, levyplus, income, hospdays, Chcond 2.
-
Si aumentamos el salario en 1 unidad tendremos 0,22 enfermedades menos en las últimas semanas. El hecho de haber tenido una prescripción médica en las últimas dos semanas aumenta la probabilidad de tener más enfermedades en las últimas dos semanas.
-
3. POSIBLES CUESTIONES 1.
2.
¿Cuál es el efecto de un año adicional de educación sobre el salario? -
0.54%. 5.4%.
-
0.54$.
-
Ninguna.
¿Cuál es el salario que se prevé para una persona con 10 años de educación? -
3.
(0.54 * 10) – ( 0 ) = 4.6
¿Cuál es la diferencia de salario que mi modelo prevé para una persona con 10 y 5 años de educación?
4.
-
(0.54 * 10) – (
0
-
(0.54 * 5) – (
0 )
⬥
Diferencia = ( 0 + (
) * 10)) – ( 0 + (
*5 )).
¿Cuantas observaciones hemos utilizado? -
526 “using observations”. 2
5.
R = 16%. El 16% de la variancia es explicada con nuestro modelo de regresión.
6.
Std. error -
“Const” = 0.68 ( Variancia estimada de 0 ). “Educ” = 0.0532 (Variancia estimada de ).
FALTA TÍTULO
8
Editor donde gretl ejecuta las comandas que escribimos para obtener así resultados: 1. 2.
“File” Archivo “Script file” Archivo de guión
3.
“New script” Nuevo guión
4.
“Gretl script” Guión de Gretl
Escribimos las siguientes comandas: -
“nulldata 100”. Obtenemos muestras de n=100. ·
-
“nulldata 2000”. Obtenemos muestras de n=2000.
“genr x=normal (0,1)”. Donde “x” sigue una distribución normal y será un vector de dimensión n=100.
-
“genr u = normal (0,1)”. L a variancia del estimador es menor que en el caso siguiente, por tanto, las estimaciones serán más precisas.
-
“genr u = normal (0,10)”. L a variancia del estimador es 10 veces más grande que en el caso anterior. La variancia de βˆ aumentará, por tanto, las estimaciones serán menos precisas. Obtenemos 1
números que se alejan más del verdadero valor (2 y 3). Genera un vector donde cada uno de los elementos se distribuye con distribución normal. -
“genr y = 3+2*x+u”
-
“ols y 0 x”. Instrucción equivalente a βˆ .
-
“loop j = l..10000 – progressive” ●
“x = normal (0,1)” “u=normal (0,1)”
●
“genr y = 3+2*x+u”
●
“ols y 0 x =”
●
“genr b1=$coeff(x)”. Manera en que Gretl entiende que quiere crear una variable que se llama b1 y corresponde al valor del estimador que obtengo (de b1).
●
“store mcl.gdt b1”
●
-
“endloop”
Clicamos el engranaje de la barra de control y pulsamos “ok”. Obtenemos así distintas estimaciones con distintas muestras, el estimador es el mismo ( βˆ0 y βˆ1 ) pero se encuentran distintas estimaciones porque las muestras son distintas. *Clicamos en el “salvavidas” de la barra de control en la derecha del todo, nos ponemos encima de la función y pulsamos con el botón izquierdo y obtendremos así, información sobre la función.
9
MATRICES -
Cogemos Wooldrige y creamos la tabla de regresores.
-
Queremos crear matrices y visualizarlas Abrimos un guión de Gretl.
-
Se me abre una página blanca y mi objetivo es encontrar el resultado de la siguiente fórmula: −1 βˆ = (X ′X) X’Y
Después de apuntar las dos primeras aplico dicha formula por pasos (primero hago lo del paréntesis y después ya hago la inversa y lo que viene a continuación) -
Escribo las siguientes formulas y le doy al print (sirve para ver los cálculos) para que muestre el cálculo de la matriz:
-
Ver los resultados de los cálculos: Le doy al engranaje
-
Ahora busco la inversa, y le doy a print
-
Le doy al engranaje para ver los resultados y…
-
¡¡ Ya tenemos la matriz de βˆ !! Le damos a print
βˆ 0 =− 0.90485 βˆ 1 = 0.54136
-
Los valores coinciden con los de la tabla inicial…
Ahora calcularemos el vector de los residuos estimados: uˆ = -
[uˆ 1 uˆ 2 . . . uˆ n ] = y − yˆ
La yˆ en formato Gretl es: yˆ = X * b . Por tanto, en Gretl para calcular el residuo lo calcularemos u = Y – X*b
Ahora calculamos la variancia del término de error: var (u1) = σ 2 σ2 =
∑ uˆ12 n−2
2
La variancia es lo mismo que σ que es la forma en la que lo escribimos en Gretl, -
Seguimos escribiendo y le damos al engranaje.
-
¡Seguimos escribiendo para ver la suma de los residuos al cuadrado y no lo pongo a continuación si no que lo meto en medio de lo que ya tenía escrito, fíjate! +Y le doy al engranaje
11
-
Seguimos escribiendo…+ engranaje Print vb: Queremos ver la matriz vb
-
Calculamos STC (ya que ya tenemos SRC) para poder así calcular r2
-
Ahora calculamos r2
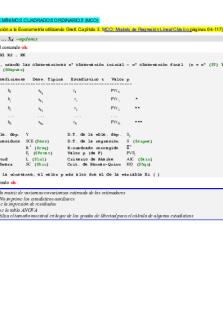
CONTRASTE DE HIPOTESIS CON GRETL
12
-
Abrimos Gretl
-
Vamos a “Archivo” , “Abrir archivo de datos “ , “Archivo de muestra” y hacemos la tabla:
Interpretación valores que usaremos para el contraste: -
Los coeficientes: Son las estimaciones de los valores de los parámetros
-
Desviación típica: Error estándar de βˆ0 y βˆ1
-
Valores de los Estadísticos t: Son los estadísticos que encontramos, es decir,
βˆ Desviación tipica
para la
hipótesis nula de H0 = B1 = 0 Cálculo “t” a partir de la hipotesis nula -
El cálculo se realizaría así:
0.0307219 0.0118111
= 2,601
Rechazamos H0 o no rechazamos H0 -
Para saber si tenemos que rechazar o no la hipótesis nula debemos comparar el valor del estadístico “t” (2.601) con el valor crítico de la distribución t que nos interesa. En este caso, suponemos que =0,05
Vamos a buscar con Gretl los valores críticos: Volvemos a la página principal de Gretl y vamos a “Herramientas”, “Tablas estadísticas”, seleccionamos la “distribución t” con grados de libertad de n-2 (526-2 =524), con una probabilidad en la cola derecha de α/2 (0,025). Le damos a aceptar y nos da el valor crítico, que es de 1,9645.
13
-
Ahora vamos a hacer el contraste. ¿Rechazamos o no la hipotesis nula? 1,96 < 2,6 Rechazamos la hipótesis nula de que B1=0. Esto significa, que los años de experiencia es una variable relevante para explicar el salario.
Vamos a realizar otro contraste con otras hipótesis Vamos a mantener los valores de la tabla y el valor crítico del ejemplo anterior. -
Este contraste se basará en determinar si un año más de experiencia provoca un aumento de 1 en el salario. H0: B1=1
H1: B1≠ 1
−1 Por lo tanto, el estadístico de contraste “t” en este caso sería: │ 0,0307219 │ = 8,20650. 0,0118111
Como 8,20650 > 1,96 (valor crítico) Rechazo la hipótesis nula de que B1=1 .
14...
Similar Free PDFs

Tutorial Gretl
- 14 Pages

guia de rapida de gretl
- 22 Pages

Tutorial
- 17 Pages

Tutorial-4 - Tutorial Problems
- 3 Pages

BFW2401-Tutorial 8 - Tutorial
- 2 Pages

Tutorial
- 2 Pages

203-tutorial-9 - Tutorial 9
- 4 Pages

Radiation tutorial
- 3 Pages

Tutorial Questions
- 15 Pages

VisiRule Tutorial
- 42 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu