Vectorial Unidad 1 v1 - Ejercicios para site PDF

| Title | Vectorial Unidad 1 v1 - Ejercicios para site |
|---|---|
| Author | Ricardo Navarrete |
| Course | Calculo vectorial |
| Institution | Instituto Tecnológico de Tijuana |
| Pages | 50 |
| File Size | 1.8 MB |
| File Type | |
| Total Downloads | 476 |
| Total Views | 901 |
Summary
Sección 12. ¿Las siguientes cantidades son vectores o escalares? Explique. a) El costo de un boleto de teatro.Escalar porque es un costo fijo, no varía.b) La corriente en un río.Vectorial, porque tiene una velocidad y dirección variable.c) La trayectoria de vuelo inicial de Houston a Dallas.Vectoria...
Description
Sección 12.2 1. ¿Las siguientes cantidades son vectores o escalares? Explique. a) El costo de un boleto de teatro. Escalar porque es un costo fijo, no varía.
b) La corriente en un río. Vectorial, porque tiene una velocidad y dirección variable.
c) La trayectoria de vuelo inicial de Houston a Dallas. Vectorial, porque tiene una velocidad y dirección variable.
d) La población del mundo. Escalar porque aunque es un valor cambiante, no tiene dirección.
2. ¿Cuál es la relación entre el punto (4,7) y el vector ? Ilustre con un bosquejo Ambos se encuentran en el primer cuadrante, por lo tanto son positivos; además el valor de su magnitud que es de √ 65 .
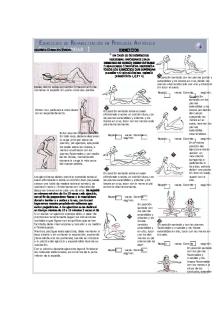
5) Copie los vectores de la figura y empléelos para dibujar los siguientes vectores.
a) u+v
b) u-v
c) v+w
u
v
a)
b)
d)
d) w+v+u
w
c)
6. Copie los vectores de la figura y utilícelos para dibujar los siguientes vectores. a) a + b
b) a – b
c) 2a
d) -1/2b
e) 2a + b
f) b – 3a
7-12 Encuentre un vector a con la representación dada por el segmento de recta dirigido AB y la representación equivalente empezando en el origen. 7.
A (2, 3), B(−2, 1 ) AB=B− A= (−2, 1) − ( 2, 3 ) = ⟨−4,−2 ⟩
AB . Dibuje
8. A(-2,-2), B(5,3)
11) A (0,3,1) B(2,3,-1)
12. A(4,0,-2) B(4,2,1).
13-16 Encuentre la suma de los vectores dados e ilustre geométricamente. 13.
⟨−1,4 ⟩ , ⟨ 6, −2 ⟩
⟨−1,4 ⟩ + ⟨ 6,−2 ⟩= ⟨ 5,2 ⟩
14. a = =
17) a = b =
a + b = (5-3), (-12-6) =
18. Encuentre a + b, 2a + 3b, |a|
y |a−b| .
a = 4i + j, b = i – 2j a + b =4 i+ j+i−2 j=5 i− j 2 a+3 b=11 i−4 j
|a|= √ 4 2a + 3b = (10,-24) + (-9-18) =
|a|= √ (( 5) 2 +( −12) 2) = √25 + 144 =√ 169 =13 |a−b|= ( 5+3 ) , (−12+6 ) =¿ 8 ,−6 >¿ √ ( 8 ) + ( 6 ) = √ 100 =10 2
17-20 Encuentre
19.
2
a + b ,2 a +3 b ,|a| y|a – b|
^ ^j+5 ^k a = ^i+ 2 ^j−3 ^k , b=−2i− ^ ^j−3 ^k + (−2 i− ^ ^j+5 ^k ) =−i+ ^ ^j+2 ^k a + b=i+2 ^ ^j−3 ^k ) +3 (−2 ^i− ^j+5 ^k ) = ( 2−6 ) ^i+( 4−3 ) ^j+ (−6+15 ) ^k=¿ 2 a +3 b=2 ( i+2
^ ^j+ 9 ^k −4 i+
|a|= √ 1 +4 + 9 =√14 ^ 2 ^j−3 k^ −( −2 ^i− ^j+5 ^k )|=|3 i+3 ^ ^j−8 k^|= √ 9+ 9+64=√ 82 |a – b|=|i+
20. a=2i - 4j + 4k, b=2j - k
a+b = (2i - 4j + 4k) + (2j - k) = 2i + 0i - 4j + 2j + 4k - k = 2i - 2j + 3k
2a+3b = 2(2i - 4j + 4k) + 3(2j - k) = (4i - 8j + 8k) + (6j - 3k) = 4i - 2j + 3k
|a| = √(2)^2 + (-4)^2 + (4)^2 = √36 = 6 |a-b| = 2i - 4j + 4k - 2j +k = 2i -6j + 5k = √(2)^2 + (-6)^2 + (5)^2 = √65
23) Halle el vector unitario que tenga la misma dirección que el vector dado
A =¿ 8 ,−1,4>¿
|A|= √ ( 8) 2 +( 1 ) 2+ (4 )2=√ 81=9 A 1 = ¿ |A| 9
24. Determine un vector que tenga la misma dirección que pero tiene longitud de 6. v =
√ (−2) +( 4 ) + (2 ) =√ 24
|v | =
2
⟨√ ⟨√
u=
−2 4 2 , , 24 √24 √ 24
r= 6
25. Si
2
2
⟩ ⟩
−2 4 2 ,6 ,6 = ⟨ −2.44,4 .89,2.44 ⟩ 24 √ 24 √ 24
v se encuentra en el primer cuadrante y forma un ángulo
π 3
con el eje x positivo y
|v |=4 , determine v en forma de componentes.
( π3 ) =2 π v =4 sen( ) =2√ 3 3 v x =4 cos
y
^ √ 3 ^j v =2 i+2
26. Si un niño jala un trineo por la nieve con una fuerza de 50N ejercida a un ángulo de 38º arriba de la horizontal, encuentre las componentes horizontal y vertical de la fuerza.
Cosθ = O/H despejando O = Hcosθ O = 50Ncos38º
Senθ = A/H despejando A = Hsenθ A = 50Nsen38º
O = 40.45N
A = 29.38N
R = 40.45Ni + 29.38Nj
29) Encuentre la magnitud de la fuerza resultante y el ángulo que forma con los ejes.
Ax = Cos 60 ( 200 ) = 100
Ay = Sen 60 ( 200) = 173.20 Bx = Cos 180 ( 300 ) = - 300 By = Sen 180 ( 300 ) = 0
Σ Ax + Bx = - 200 Σ Ay + By = 173.20
√ (−200 ) + ( 173.20) 2
θ=arctan
(∑ ∑
2
=264.571
)
Ay + By =−49.10 Ax + Ay
30. La magnitud de un vector de velocidad se llama rapidez. Suponga que un viento sopla desde la dirección N45ºW a una rapidez de 50 km/h. Un piloto dirige un avión desde la dirección N60ºE a una rapidez de 250 km/h.
Vx =50cos(135º) Vy =50sen(135º) Ax =250cos(60º) Ay =250sen(60º) Rx = 89.64 Ry = 251.86 R =267.33 km/h θ=70.4 °
31. Una mujer camina al oeste en la cubierta de un barco a 3 millas/h. El barco se mueve al norte a una velocidad de 22 millas/h. Encuentre la rapidez y la dirección de la mujer respecto a la superficie del agua. m =−3 i^ b=22 ^j r = m + b=−3 ^i+22 ^j
|r|= √484+9= √493 ; θ=tan−1
( −322 )=−82.234 …
Rapidez ≈ 22.2 millas/h Dirección ≈ 7.76º al oeste del norte
32. Cuerdas de 3m y 5m longitud están atadas a un estrella decorativa suspendida sobre una plaza principal. La decoración tiene una masa de 5Kg. Las cuerdas, sujetadas a distintas alturas, forman ángulos de 52º y 40º con la horizontal. Encuentre la tensión en cada alambre y la magnitud de cada tensión.
F = m*g = 5Kg*9.81m/s^2 = 49.05N → 49N T1 = -3cos52º + 3sen52º = 0.48i + 2.95j T2 = 5cos40º + 5sen40º = -3.33i + 3.72j
Tx = -T1cos52º + T2cos40º = 0 → despejando T2 = T1cos52º / cos40º Ty = T1sen52º + T2sen40º = 49N
T1sen52º + T2sen40º = 49N T1sen52º + (T1cos52º / cos40º) = 49N sen40º T1sen52º + T1cos52ºtan40º = 49N T1(sen52º + cos52ºtan40º) = 49N T1 =
49N
= 37.55N
(sen52º + cos52ºtan40º) T2 = T1cos52º = 30.18N cos40º
Sección 12.3 2. Encuentre el producto punto de dos vectores si sus longitudes son 6 y π . 4
1 3
y el ángulo entre ellos es
|b|= 1
|a|=6 ;
;
3
θ=
π 4
( 3) ( 4 )
|a||b|cos ( θ )= 6· 1 cos π = √2
3–10 Encuentre
a · b .
3. a = , b = a*b = , ¿ 13 st
7. a= i – 2j +3k
b=5i +9k
a · b=5+0+27 = 32
^ 4 ^j+6 k^ 8. a =4 ^j−3 k^ , b=2 i+ a · b= (2 · 0 ) +( 4 · 4 ) +( −3 · 6) =0+16 −18=−2
9. |a| = 6, |b| = 5, el ángulo entre a y b es 2�/3 a*b = |a| |b| cosθ a*b = 6*5 cos2�/3 a*b = -15
13. demuestre que i · j= j · k= k · i=0 Si a · b= |a||b|cosθ Donde a · b=0 si θ =90º Entonces debido a que θ
ij
= θ
jk
= θ
i · j= j · k= k · i=0 demuestre que i · i= j · j= k · k=1
ki
=90º
si a · b= |a||b|cosθ donde a · b= |a||b| =0 si entonces debido a que
θ
ii
θ =0º
= θ
jj
= θ
kk
=0º y
|i |=| j|=|k |=1
i · i= j · j= k · k=1
14. Un vendedor ambulante vende a hamburguesas, b hot dogs y c bebidas carbonatadas en un día específico. Cobra $2 por una hamburguesa, $1.50 por un hot dog y $1 por una bebida carbonatada. Si A=⟨ a , b , c ⟩ y P= ⟨ 2,1.5, 1⟩ , ¿cuál es el significado del producto punto A· P ? P =( a· 2 ) + (b·1.5 ) + ( c·1 )=2 a+ 1.5 b + c A· El producto punto significa la ganancia total.
15–20 Encuentre el ángulo entre los vectores. (Primero encuentre una expresión exacta y luego aproxime hasta el grado más próximo.) 15. a = , b = <
√ 7 ,3>¿
2
2
6¿ ¿ |a| = −8 ¿2 +¿ ¿ √¿ a*b = < (-8)( cosθ = θ=
√7
|b| =
3¿ ¿ √ 7 ¿2+¿ ¿ √¿
) + (6)(3) = -3.1660
a∗b /¿ a ∨¿ b ∨¿−3.1660 /(10 )( 4)=−0.07915
co s−1 (−0.07915)=94.53 º
18) ,
8 =52.78 | √35||√ 5|
θ=arcos
19. a=j + k, b= i + 2j – 3k a· b |a||b|
cosθ=
a · b=2-3=1
|a|= √ 2 |b|= √ 14 cosθ=
−1 =0.1889 2 √ √ 14
θ=1.76=100.89 °
20.
^ k^ a = ^i+ 2^j−2 k^ , b=4i−3
|a|= √ 1 +4 + 4 =3 ; |b|= √ 16 +9=5 a · b= (1 · 4 ) + ( 2· 0 ) +(−2 ·−3 )=4 + 0 + 6=10 θ=cos
( )
−1
a · b −1 10 =cos ≈ 48.189 ° 15 |a||b|
( )
21. A(1,0), B(3,6), C(-1,4)
AB = =
|AB| = 2
10 ¿ √¿
BC = =
|BC| = 2
√5
AC = =
|AC| = 2
√5
2 10 5 (¿)=45º cosθ = AB*BC / |AB| |BC| = (2)(-4) + (6)(-2) / (2 ¿ )(2 ¿ ) → θ = 1 /√ ¿ √¿ √¿ −1 co s ¿ 10 5 cosθ = AB*AC / |AB| |AC| = (-2)(2) + (4)(6) / (2 ¿ )(2 ¿ ) → θ = √¿ √¿ cosθ = BC*AC / |BC| |AC| = (-4)(-2) + (-2)(4) / (2
5 5 ¿ )(2 ¿ ) → θ = √¿ √¿
2 (¿)=45º 1 /√ ¿ co s−1 ¿ co s−1 (0)=45 º
24) Determine si los vectores dados son ortogonales, paralelos o ninguno
a)
u · v=−12−108−48=−168 ∴ No ortogonales −3 −9 −6 = = ∴ Son paralelos 12 8 4 b)
u · v=2+1+2=5 ∴ No son ortogonales
1 ≠−1 ≠ 2 ∴ No son paralelos 2 c)
u · v=−ab+ab+ 0=0 ∴ Son ortogonales
25. Use vectores para decidir si el triángulo con vértices P(1,-3,-2), Q(2,0,-4) y R(6,-2,-5) a= QR =
b= QP =
c= PR =
a · b=-4 + 6 -2=0 b · c=-5-3-6=-14 c · a=20-2+3=21 Debido a que a · b=0
θ
cb
=90º
de modo que es un triángulo rectángulo.
26. ¿Para qué valores de b son ortogonales los vectores Si: a = ⟨−6, b , 2⟩
y
⟨−6, b , 2 ⟩ y ⟨ b , b2 ,b ⟩ ?
b= ⟨ b , b2 ,b ⟩
Para que los vectores sean ortogonales, entonces: a · b=0 Por lo tanto: a · b= (− 6 ·b )+ ( b·b2) +( 2 · b ) =−6 b+b3 +2 b=b3 −4 b=b (b2−4 )=¿ b ( b−2 ) (b+2 ) Los vectores a y b son ortogonales para los valores de b=0,2,−2
27. Encuentre un vector unitario que es ortogonal a i + j e i + k.
|i
j
k|
|1
1
0| = i [(1)(1) - 0] - j[(1)(1) - 0] + k[(1)(0) -(1)(1) = i - j + k
0
12+ 12+12 ¿ →a=1/ 1| = ¿ √¿
|1
√3
Halle los cosenos directores y los ángulos directores del vector. (Dé los ángulos directores correctos hasta el grado más próximo.)
30) Halle los cosenos directores y los angulos directores del vector
|a|= √ 6 cos a=
()
1 1 =65.90 ° a=arcos 6 √6
( ) −1 −1 γ=arcos( cosγ= =0.99° √6 √6) cos β=
−2 −2 =144.73° β=arcos 6 √ √6
33. , donde c > 0
c 2+ c 2+ c 2 ¿ ¿ √¿ cos ⍶ = cos� = cossℽ=
co s−1 (1 / √3) = 54.73
29–33 Halle los cosenos directores y los ángulos directores del vector. (Dé los ángulos directores correctos hasta el grado más próximo.) 31. a = 2i+3j-6k
|a|= √ 4 +9+36 =7 cos ∝=0.285 ∝=1.25 rad ≈ 73.44 ° cosβ=0.428 β=1.12 rad ≈ 64.62 ° cosγ=−0.857 γ =2.6 rad ≈ 148.99 °
32.
2 ^i− ^j+2 k^
|v|= √ 4 +1 + 4 =3 cos ( α )=
−1 3
2 3
cos ( β )=
( 23 )=48.19 °
β=cos−1
α=cos−1
cos ( γ )=
( −13 )=109.47 °
c 2+ c 2+ c 2 ¿ ¿ √¿ cos ⍶ = cos�= cossℽ=
co s−1 (1 / √3) = 54.73
35–40 Encuentre el escalar y las proyecciones vectoriales de 36) A B
|a|= √ 9+16=√ 25=5 compB= proyB=
15 =3 5
9 12 15 3 i−4 j= i− j 25 5 5
( 23 )=48.19 °
γ =cos−1
33. , donde c > 0
b sobre a .
2 3
37. a=, b= a· b 3+ 12−6 9 = =1.2857 = |a| √9+36+4 7
compab= proyab=
38.
a· b
|a|
2
a=
27 54 18 9 3+12 −6 a= a= , ,− 49 49 49 49 9+36+4
a = ⟨−2, 3,−6 ⟩ , b= ⟨5 ,−1, 4 ⟩
|a|= √ 4 +9+36 =7 a · b= (− 2· 5) + (3 ·−1 ) + (−6 · 4) =−10−3 −24 =−37 a· b −37 compa b= = |a| 7 −37 a · b a= ⟨ −2, 3 ,−6 ⟩ = 1 ⟨ 74 ,−111, 222⟩ 2 49 7 (|a|)
proya b=
39. a = 2i - j + 4k, b = j + 1/2k
a = 2i - j + 4k → →
√ 22+ 12 + 42=√ 21
compa b = a*b / |a| = [(0)(2) + (1)(-1) + (½)(4)] /
√ 21
proya b = 1/
* a/|a| = a/
√ 21
= 3
, 4/
√ 21
>
44. Suponga que a y b son vectores no nulos. (a) ¿Bajo qué circunstancias a · b b · a = |a| |b|
Cuando Como
compa b=compb a ?
a · b= b· a
Entonces compa b=compb a cuando |a|=|b| También cuando a · b= b· a =0
(b) ¿En qué circunstancias
a · b b · a a = 2 2 b ( |a|) ( |b|)
Cuando Como
proya b=proy b a ?
a · b= b· a
Entonces 1 1 b= a 2 2 (|b|) ( |a|)
Por lo tanto También
proya b=proy b a cuando
a = b o cuando son ortogonales
a · b= b· a =0
45. Encuentre el trabajo realizado por una fuerza F = 8 i - 6j + 9k que mueve un objeto del punto (0, 10, 8) al punto (6, 12, 20) a lo largo de una línea recta. La distancia se mide en metros y la fuerza en newtons.
D = PQ = = W = F * D = * = = 144J
Sección 12.4 1–7 Encuentre el producto cruz 1. a = , b=
a × b
y compruebe que es ortogonal a
a y b .
c = a x b = = c·a
= 16*6+0+48*(-2) = 96-96 = 0
c·b
= 16*0+0*8+48*0 = 0
Entonces debido a que a∙b=|a||b|cosθ Donde a∙b=|a||b|=0 si θ=0º Se demuestra que son ortogonales
2. a = ⟨1,1 ,−1 ⟩ , b=⟨ 2,4,6 ⟩ ^ ^j+2k^ a × b=i^ ( 6+4 ) − ^j ( 6 +2 ) +k^ ( 4−2 ) =10i−8 Para que sean ortogonales ( a × b ) · a=0
ó ( a × b ) · b=0
( a ×b ) · a=⟨ 10 ,−8, 2 ⟩ · ⟨ 1,1 ,−1 ⟩=10−8−2=0 3. a = i + 3j - 2k, b = -i + 5k
|i
j
k|
|1
3
2| = i[(3)(5)-(0)(2)] - j[(1)(5)-(-1)(2) + k[(1)(0)-(-1)(3) = 15i - 7j + 3k
|-1
0
5|
6)
t
−1
t
−1
a=i−e +e b=2i+e − e
i j k t−1 −1 t −1 t a ×b=1 −e e−1 =e i−e j(e −2 e )k 1 et − e−1 7. a = , b= c = a x b = = c·a
= t4(t)-2t3(t2)+t2(t3)=0
c·b
= t4(1)-2t3(2t)+3t2(t2)=0
Entonces debido a que a∙b=|a||b|cosθ
Donde a∙b=|a||b|=0 si θ=0º Se demuestra que son ortogonales
8. Si a = ^i−2k^ , b= ^j+ ^k , encuentre inician en el origen.
a × b . Trace a ,
b y a × b
como vectores que se
^ ^j+ ^k a × b=i^ ( 2 )− ^j ( 1 ) +k^ ( 1) =2i−
9. (i x j) x k ixj = k kxk = 0
12) Encuentre el vector, no con determinantes sino usando propiedades del producto cruz (i+j)x(i-j) ( i + j ) x (i)(i + j) x (-j) (i x i ) + (j x i) + ( i x (-j)) + (j x (-j)) (i x i) + ( j x i ) + (-1) ( i x j) + (-1)(j x j) = -k - k = 2k
13. Diga si cada expresión es significativa. Si no, explique por qué. En caso afirmativo, diga si es un vector o un escalar. a. a∙(b x c) es significativa y resultaría en un escalar b. a x (b∙c) no es significativa pues el producto cruz solo puede ser entre vectores y no vector y escalar.
c. a x (b x c) es significativa y resultaría en un vector d. (a∙b) x c no es significativa pues el producto cruz solo puede ser entre vectores y no vector y escalar. e. (a∙b) x (c∙d) no es significativa pues el producto cruz solo puede ser entre vectores y no entre escalares. f. (a x b) ∙ (c x d) es significativa y resultaría en un escalar
14–15 Encuentre |u ×v |
y determine si u × v
está dirigido hacia la página o hacia afuera de ésta.
|u ×v |=|a||b|sen ( θ) =5· 10 · sen ( 60 ° )=25√ 3 Está dirigido hacia la página.
|a xb| = |a| |b| sen150º = (6)(8) sen150º = 24 Usando la regla de la mano, el giro es de 0º a 180º… Por lo tanto es hacia adentro.
i j k a ×b= 3 1 2 =−2 i−2 j+2 k −1 1 0
i j k b × c=−1 1 0=−4 i−4 j 0 0 4 i j k a × c ( b × c )= −1 1 0=2 i+ 2 j + 2 k 3 1 2 i j k ( a ×b ) × c=−2 −2 2 =8 i−8 j 0 0 −4
19. encuentre dos vectores unitarios ortogonales a a= y b= c = a x b = = d = b x a = = Los vectores unitarios serian <
−2 −1 1 , , >y< √6 √6 √6
2 1 −1 , , > √6 √ 6 √ 6
40. Determine la magnitud del par de torsión respecto a P si se aplica una fuerza de 36 lb como se muestra.
Sea r
el vector que representa la distancia de P a C.
Entonces |r|= √32=4 √ 2 La fuerza que actúa sobre r es la componente del vector de 36lb que es perpendicular al vector r (llámese n ). Con el triángulo ABC podemos obtener n mediante: n=36 sen( 45°+30 ° )=36 sen (75 ° ) Aplicamos la formula |τ|=|r|| F| sen ( θ)
|τ|=4 √2· 36 sen (75 ° ) ≈ 196.7 ft·lb
41. Una llave de 30cm de largo yace a lo largo de eje y positivo y sujeta un perno en el origen. Se aplica una fuerza en la dirección y al final de la llave. Encuentre la magnitud de la fuerza necesaria para suministrar 100 N*m de par de torsión a perno.
44) Sea P un punto fuera del plano que pasa por los puntos Q,R y S. Muestre que la distancia d desde P al plano
¿ a ×b∨¿ (|a× b|· c ) d= ¿
es
donde a = QR, b = QS y c = QP
Use la fórmula del inciso a para hallar la distancia desde el punto P(2,1,4) al plano que pasa por los puntos Q(1,0,0), R(0,2,0) y S(0,0,3).
a=¿ 0−1, 2−0,0−0> ¿← 1,2,0>¿ b=¿ 0−1,0 −0,3−0>¿←1,0,3>¿ c=¿ 2−1,1−0,4 −0> ¿¿
| |
|
−1 2 0 −1 0 3 0 +6 +0 + 8 + 3 +0=17 |a ×b| · c 1 1 4
|
i j k −1 −2 0 6 i+0 j−0 k +3 j+0 i+ 2 k= 6 i+3 j+2 k (a × b ) −1 0 3 d=
|a × b|· c 17 = =2.42 7 |a ×b|
√ 36+9+ 4=√ 49=7
45. Demuestre que (a-b) x (a+b) = 2(a x b) a-b= a+b=
(a-b) x (a+b) = =
46. Demuestre la propiedad 6 del teorema 8, es decir,
(a · b ) c . a × ( b × c )= ( a · c ) b−
| |
i^ ^j ^k a × ( b × c ) = a × b x b y b z = a × [ ( b y c z−b z c y ) ^i− (b x c z−bz c x ) ^j+ (b x c y − b y c x ) ^k ] cx c y cz
|
|
^i ^j ^k ¿ ax ay az b y c z−b z c y −bx c z + bz c x b x c y −b y c x
¿ [a y (b x c y −b y c x ) −a z (−b x c z +b z c x ) ] ^i−[ ax ( b x c y −b y c x ) −a z( b y c z −b z c y )] ^j+ [ a x ( −b x c z +b z c x )−a y ( b y c z −b
Para
[ a y(b x c y −b y c x )−a z (−b x c z +b z c x )] i^ a y b x c y −a y b y c x +az b x c z− a z b z c x b x( a y c y + a z c z ) −c x ( a y b y +a z b z )
b x( a y c y + a z c z) −c x ( a y b y + a z b z )+ ax b x c x −a x b x c x b x( ax b x + a y c y + a z c z )−c x ( a x b x +a y b y + az b z )
Como a x b x +a y b y + a z b z =a · b Entonces para ^i ,
^j
y
y
a x b x +a y c y + a z c z =a · c = (a · c ) bx −( a · b ) c x
^k respectivamente
( a · c )b x − ( a · b ) c ...
Similar Free PDFs

Unidad 1 - ejercicios hechos
- 4 Pages

Unidad VI. Ejercicios 1
- 3 Pages

V1 Contenidos Unidad 1 semana 6
- 27 Pages

ejercicios de geografia unidad 1
- 2 Pages

Ejercicios Unidad 1 ERIK Robayo
- 18 Pages

Ejercicios para examen parcial 1
- 6 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu