Tema II Geometría - Lecture notes 2 PDF

| Title | Tema II Geometría - Lecture notes 2 |
|---|---|
| Course | Didáctica de la Geometría |
| Institution | Universidad de Cantabria |
| Pages | 19 |
| File Size | 998.6 KB |
| File Type | |
| Total Downloads | 50 |
| Total Views | 128 |
Summary
Profesora: Cecilia Valero...
Description
1 Tema II: Teorías de aprendizaje en Geometría 1. Las teorías más relevantes Son numerosos los estudios que en las últimas décadas han tenido como objetivo la enseñanza y el aprendizaje de la geometría en el ámbito escolar, pero una amplia mayoría se han desarrollado teniendo como punto de partida los trabajos de Piaget y de los esposos Van Hiele. -
Piaget Teoría sobre el desarrollo cognitivo Teoría sobre el desarrollo de los conceptos geométricos
-
Van Hiele Teorías de enseñanza-aprendizaje de la geometría o Niveles de razonamiento o La importancia del lenguaje o La secuencia del aprendizaje
2. Aspectos evolutivos en el niño para la concepción del espacio y la geometría. Teoría de Piaget -
-
-
-
Aspectos positivos en la formación del individuo por la realización de actividades geométricas. Trabajos afirman que ciertos errores o dificultades en el aprendizaje en los diversos niveles de Primeria se producen por no haber desarrollado determinadas habilidades geométricas en los niveles precedentes. Como en otras áreas, también en geometría muchos psicólogos (Piaget, Bruner, Dienes) opinan que la manipulación de objetos concretos constituye la base del conocimiento. Las acciones físicas deben interiorizarse en forma de conceptos, símbolos o figuras. Las primeras interacciones del niño con su entorno, previas al desarrollo del lenguaje, se basan casi exclusivamente en experiencias percibidas, en un alto porcentaje, por medio de la vista y del tacto y tienen relación con el espacio. Cuando se desarrolla el lenguaje, las palabras que describen conceptos espaciales adquieren significado en el entorno físico. Sin embargo, la percepción que el niño tiene del espacio; los criterios a los que es sensible y se refiere, los que ocasionalmente adopta; los caracteres que le permiten identificar, reconocer o relacionar un objeto o un hogar; las propiedades que va a retener y usar para construir su propia representación del espacio y para actuar sobre él, evolucionan con la edad y el grado de maduración.
2.1. Teoría del desarrollo cognitivo según Piaget Piaget distingue: Cuatro etapas de desarrollo cognoscitivo progresivo en el niño: -
Pensamiento no reflexivo y no sistemático (estadio 1/periodo sensorio-motor): conocimiento de los objetos físicos que le rodean Pensamiento empírico (estadio 2/período pre-operacional): hay representación mental y se desarrolla la función simbólica, pero no hay rigor de operaciones lógicas
-
Lógico-deductivo (estadios 3-4/operaciones concretas – operaciones formales resp.): adquiere un pensamiento lógico referido a objetos concretos y del momento presente. Alrededor de los 11 años, opera lógica y sistemáticamente con símbolos abstractos, sin tener necesariamente una relación directa con los objetos del mundo físico
Dos tipos de conocimiento: -
La percepción: conocimiento práctico de los objetos que se obtiene como resultado de la interacción directa con ellos (estadio I) La representación: capacidad del niño para razonar sobre las propiedades espaciales de un objeto cuando ya no está presente
Piaget estudia el desarrollo del conocimiento espacial asociado a la propia evolución del niño, en interacción con el entorno. Uno de los aspectos más reseñables de las aportaciones de Piaget tiene relación con el orden en el que el niño adquiere las propiedades geometréticas. 2.2. Algunas consideraciones acerca de las propiedades topológicas, proyectivas y euclídeas Recordemos: 1.1.1.1 Geometría
Un conjunto (objetos, elementos, puntos) + Grupo de transformaciones (cambios) que actúan sobre los objetos del conjunto
Propiedades invariantes
Transformaciones:
Deformaciones (sin rupturas)
Proyecciones (figura/sombra)
Semejanzas y movimientos
ESPACIO Conjunto (objetos, elementos, puntos)
Ejemplo
Propiedades invariantes, que permanecen
Continuidad: conexión entre puntos; línea abierta o cerrada; intersección de líneas; frontera, interior y exterior de una región; número de agujeros de una región; número de bordes y de caras de una superficie.
Continuidad; conexión entre puntos,… + Linealidad, convexidad
GEOMETRÍA PROYECTIVA
TOPOLOGÍA
Propiedades que no permanecen
Figuras equivalentes a la del ejemplo
Convexidad, paralelismo, perpendicularidad, linealidad, longitudes, ángulos.
Continuidad; conexión entre puntos,… Linealidad,… + Proporcionalidad o igualdad según sean semejanzas o movimientos. En consecuencia, ángulos y paralelismo. GEOMETRÍA EUCLÍDEA
Distancias, paralelismo, amplitud de ángulos.
Para semejanzas, distancias. Para movimientos, nada (todo permanece).
Algunas actividades ilustrativas. ¿Podrían adaptarse para ser llevadas al aula escolar? ¿Estaría justificado? ACTIVIDAD 1. Indica en cada caso si son topológicamente equivalentes los objetos mostrados en las imágenes.
ACTIVIDAD 2. Considera tres tiras de papel iguales.
Una déjala como está. En la otra, pegamos los lados cortos, de manera que se identifiquen A y D y B y C respectivamente. Y en la tercera, pegamos los lados cortos, de manera que se identifiquen A y C y B y D respectivamente.
La figura muestra el proceso relizado tras el cual se obtiene: una tira, una superficie cilíndrica y una banda o cinta de Moebius. ¿Cuántas caras tiene cada una de las figuras anteriores? ¿Y cuántos bordes? ¿En cuántas piezas quedará dividida cada figura si efectuamos un corte longitudinal? Partiendo con una orientación y tras recorrer una cara, ¿la orientación permanece? Recoge las respuestas en la tabla siguiente. Nº caras Tira Sup. cilindro Cinta
Nº bordes
Nº piezas tras corte
Orientable
¿Son topológicamente equivalentes las figuras anteriores?
ACTIVIDAD 3. Compara la imagen de una foto con el escenario real que ha sido fotografiado: ¿los ángulos de la foto tienen la misma amplitud que los correspondientes en el objeto real? Si hay elementos paralelos en el ambiente real, ¿son paralelas sus imágenes correspondientes? Hazte preguntas similares a las anteriores y trata de responderlas.
ACTIVIDAD 4. La figura representa un foco de luz puntual, una regla de madera con un pequeño agujero en su punto medio y una pared.
a) Representa sobre la pared la sombra de la regla, indicando el punto brillante que se produce como consecuencia de la filtración de luz a través del agujero. ¿Está ese punto en la mitad de la sombra? b) Si se cambia de posición la regla, de manera que siga dando la misma sombra, ¿cambiará el punto de luz en la sombra? c) ¿Se puede decir que en la geometría proyectiva se conservan los puntos medios? ACTIVIDAD 5. Considera la imagen siguiente. a) En ella, las figuras F1, F2, F3 y F4 se han obtenido tras someter a F a ciertas transformaciones. Indica cuál es la transformación utilizada en cada caso. b) De Matemáticas para Maestros, conocer el significado de figuras semejantes. ¿Crees que son semejantes F2 y F4? c) ¿Dentro de qué tipo de geometría estás trabajando ahora?
ACTIVIDAD 6. Abajo se muestran dos planos del metro de Madrid. No abarcan exactamente la misma zona, pero analiza la parte común.
a) ¿Son idénticas esas partes? b) ¿Cuál es lo más importante es un plano de estas características? c) ¿Qué tipo de propiedades geométricas son las que se tienen en cuenta a la hora de confeccionar un plano de metro? ACTIVIDAD 7. ¿Cuál es la diferencia más reseñable entre las dos obras pictóricas siguientes? ¿La encajas en algún tipo de geometría?
ACTIVIDAD 8. Se trata de colorear el dibujo de manera que se emplee un solo color para cada parte del mismo y que no haya dos partes adyacentes con igual color. a) Claramente, con 8 colores diferentes es posible colorear la figura ajustándose a las normas establecidas, ¿pero cuál es el menor número de colores necesarios? b) Modifica el dibujo como creas conveniente, para que el número mínimo de colores necesarios sea uno más que el determinado en a). En ambos casos, usa para la justificación lo que se denomina un grafo: conjunto de puntos que simbolicen las partes del dibujo, unidos por segmentos en los casos que representen partes adyacentes. ¿Qué tipo de propiedades son relevantes en esta situación: topológicas, proyectivas o métricas?
. ACTIVIDAD 9. En las actividades 1 y 2 anteriore se han trabajado, respectivamente, la equivalencia topológica, o no, entre líneas y la equivalencia topológica, o no, ebtre superficies. Avancemos un poco más. En diferentes páginas divulgativas, se dice, a modo de introducción simpática, que un topólogo es una persona que no distingue un donut de una taza de café. 2.3. Piaget y el desarrollo de los conceptos geométricos Piaget sostiene que la percepción que el niño tiene del espacio hace referencia, en primer lugar, a criterios de carácter topológico, después de orden proyectivo y finalmente de tipo métrico.
Piaget sostiene que la percepción que el niño tiene del espacio hace referencia, en primer lugar, a criterios de carácter topológico, después de orden proyectivo y finalmente de tipo métrico. Ante una sucesión de figuras como estas cabría esperar que un niño. - en la etapa topológica distinguiera sólo el anillo de las demás (pues tener un agujero está relacionado con “cerramiento”). - al adquirir la etapa proyectiva, distinguiría el círculo del cuadrado y paralelogramo (por ser la “rectitud” una propiedad proyectiva). - finalmente, distinguiría entre el cuadrado y el paralelogramo por ser el tamaño del ángulo una propiedad euclídea. Pero hay estudios que indican que no es exactamente así. Por ejemplo, Lovell muestra su desacuerdo en su obra Desarrollo de los conceptos básicos y científicos en los niños. Es cierto que las primeras percepciones espaciales hacen referencia a propiedades globales, independientes de la forma o el tamaño. Sin embargo se entiende que los estadios
madurativos de Piaget no son, tal y como él defiende, disjuntos ni están determinados absolutamente, sino que entre ellos se superponen diferentes modos de percepción, de manera que el niño percibe criterios topológicos, proyectivos y métricos simultáneamente.
3. Teoría de la enseñanza-aprendizaje de la geometría. El modelo de Van Hiele 3.1. Niveles de desarrollo La teoría de los esposos Van Hiele, que puede considerarse como una teoría evolutiva de enseñanza-aprendizaje de la geometría, comprende cinco niveles de desarrollo en la comprensión de los conceptos geométricos que, a diferencia de los estadios de Piaget, sí están influenciados por el currículo escolar. N1. Visualización El estudiante identifica una figura por su apariencia, como un todo, pero no establece relaciones entre los elementos que la determinan. ! Por ejemplo, en la situación de la imagen, sabe decir qué figura es cuadrado pero no es capaz de verbalizar que en el caso del cuadrado los lados son iguales y no así en el rectángulo. ! Las formas se distinguen por su apariencia global.
N2. Análisis En este nivel el estudiante empieza a desarrollar una conciencia sobre las partes de la figura, puede establecer algunas propiedades de las mismas pero no es capaz de ver las relaciones entre esas propiedades. Por ejemplo, puede reconocer que un rectángulo tiene cuatro lados, los lados opuestos son iguales en longitud y tiene cuatro ángulos rectos; o quizás pueda “deducir” que en un rombo los ángulos opuestos son iguales; pero no es capaz de ver el cuadrado como una clase especial de rectángulo o de rombo. En este nivel, es poco probable que los niños relacionen diferentes formas. N3. Deducción informal
El estudiante empieza a organizar los descubrimientos del nivel anterior, puede usar de manera informal la lógica para deducir propiedades de las figuras y reconocer una figura por sus propiedades a través de razonamientos. Por ejemplo, si observa que un cuadrilátero tiene un par de lados paralelos e iguales, puede concluir que la otra pareja de lados tiene esas mismas características; o puede comenzar a establecer generalizaciones del tipo cada cuadrado es un rectángulo. Otro ejemplo de deducción informal es la que un estudiante realiza cuando, tras constatar que los ángulos interiores de los polígonos convexos regulares van aumentando con el número de lados e ir construyendo “rincones” con polígonos regulares iguales, afirma que no va a poder construir poliedros regulares con caras hexagonales, heptagonales, octogonales, etc. N4. Deducción formal En este nivel se entiende el sentido de los axiomas, de los teoremas, las definiciones. Pueden llegar a realizar demostraciones formales, viendo su necesidad para justificar las propiedades formuladas. N5. Rigor El razonamiento se hace rigurosamente deductivo, se es capaz de razonar sin ayuda de la intuición, de ejemplos concretos. Se alcanza el más alto nivel de rigor matemático.
A continuación se muestran algunos ejemplos, en el contexto de los polígonos, para ilustrar el tipo de actividades que se entienden como propias de los tres primeros niveles, que son los que realmente interesan en este curso. 3.1.1
Características de actividades del Nivel 1. Ejemplo: Características de las actividades Ejemplo de actividad - Actividades de clasificación, - Selecciona una forma al azar y identificación y descripción de formas encuentra otras parecidas. variadas. - ¿Qué rasgo tienen las formas para - Uso de gran cantidad de modelos considerarlas similares? físicos que se puedan manipular por los niños. - Ejemplos de una variedad amplia de formas diferentes.
-
Dar oportunidades para que los alumnos construyan, dibujen, compongan o descompongan figuras diversas.
-
-
Dibuja una nueva forma que se ajuste a la categoría y explica por qué es de esa clase. Da el nombre de las formas de esa categoría si lo conoces.
3.1.2
Características de actividades del Nivel 2. Ejemplo: Características de las actividades Ejemplo de actividad - Actividades centradas en las Clasificar las formas por nombres de propiedades de las figuras, y no en la propiedades (y no por nombres de las simple identificación. formas). Por ejemplo: - Resolver problemas en los que las - ¿Cuáles son las formas propiedades de las formas hayan de que tienen lados ser tenidas en cuenta. opuestos paralelos? - Uso de modelos físicos manipulables - ¿Cuáles de ellas tienen y que permitan explorar las diversas además un ángulo propiedades de las figuras. recto? (cuadrados, - Clasificar figuras utilizando sus rectángulos que no propiedades y sus nombres. sean cuadrados…). - ¿Cuál es el nombre de esta clase de figuras? Diferencias entre el nivel 1 y el nivel 2: - En el nivel 1, se pueden haber clasificado unos triángulos como “grandes” y “pequeños”, “puntiagudo” o “no puntiagudo”, o “con esquinas cuadradas” y “sin esquinas cuadradas”. - En el nivel 2, el mismo conjunto de triángulos se puede clasificar según el tamaño relativo de los ángulos o la longitud relativa de los lados. Algunas actividades adecuadas para el nivel 1 se pueden extender al nivel 2 cambiando las variables de la tarea.
3.1.3
Características de actividades del Nivel 3. Ejemplo: Características de las actividades Ejemplo de actividad - Continuar usando propiedades de los ¿Cuál de las siguientes frases es relevante modelos, pero con la atención puesta para caracterizar la imagen de la figura? en la definición de propiedades. Lados opuestos iguales - Comenzar a usar un lenguaje de Cuatro ángulos iguales naturaleza deductivo aunque Diagonales de igual longitud informal: todos, algunos, ninguno, si Lados opuestos paralelos entonces, qué ocurre si, etc. - Investigar la validez de enunciados recíprocos. Por ejemplo: “Si una figura es un cuadrado, debe tener cuatro ángulos rectos.” ¿Es cierto su recíproco, es decir “si una figura tiene
-
-
cuatro ángulos rectos, entonces debe ser un cuadrado”? Usar modelos y dibujos y comenzar a buscar generalizaciones y contraejemplos. Estimular la formulación y demostración de algunas hipótesis.
3.2. Propiedades que caracterizan el modelo 3.2.1 Algunas propiedades del modelo Secuencial Avance Intrínseco – extrínseco Lingüística
Los Van Hiele además de establecer los niveles mencionados, han identificado algunas propiedades que caracterizan el modelo y que deben servir al educador para planificar la instrucción.
Concordancia Secuencial Para que una persona trabaje bien en un nivel determinado, debe haber adquirido las estrategias del nivel precedente. Avance El paso de un nivel a otro no es automático y más que de la edad depende de la correcta superación del nivel anterior. Intrínseco – extrínseco Los objetos inherentes a un nivel se transforman en objeto de estudio en el nivel siguiente. Ejemplo: En el nivel 1 se percibe una figura de manera global, pero los componentes y las propiedades que la determinan no se analizan hasta el nivel 2. Lingüística Cada nivel tiene sus propios símbolos lingüísticos y sus propios sistemas de conexión entre estos símbolos. Por eso una relación que puede ser correcta en un nivel quizá deba ser modificada en el nivel siguiente. Ejemplo: En el nivel 2 puede no entenderse que un cuadrado también es un paralelogramo y un rectángulo, pero el ver esta inclusión de clases es fundamental que sea tratado en el nivel 3. No se trata sólo de adquirir conocimientos matemáticos sino también de mejorar y ampliar las capacidades referidas al lenguaje necesario en cada nivel.
Una palabra puede tener significados diferentes en los diferentes niveles, es decir, a cada nivel de razonamiento le corresponde un lenguaje específico. Concordancia Ha de haber sintonía entre el nivel del estudiante y el de la instrucción. Si el estudiante está en un nivel y la instrucción en otro diferente, puede que no se dé el aprendizaje y el progreso deseados. En particular, si el profesor, los materiales, el contenido, el vocabulario, y todo lo demás, están en un nivel superior al del alumno, el estudiante no será capaz de seguir el proceso de pensamiento utilizado. 3.2.2 Ejemplos sobre el uso del lenguaje en los diferentes niveles de razonamiento Actividad 1. Señalar de entre estos polígonos los que son regulares.
Un alumno del nivel 1 clasificó como polígonos regulares los números 1, 3, 4 y 5 por resultarle “familiares” y como polígonos irregulares el resto por ser “formas extrañas”. Las razones de los estudiantes en nivel 2 para su clasificación se basaron e igualdad de ángulos y/o lados.
Actividad 2. Escribe en la imagen una P en los polígonos, una N en los no polígonos. Escribe una T en los triángulos, y una C en los cuadriláteros. Explica por qué.
Respuesta nivel 1: “La forma 2 no es un polígono porque no sigue ninguna regla y la forma 7 es un cuadrilátero porque es un rombo con sus diagonales y paralelas”.
Respuesta nivel 2: “La forma 8 no es un polígono porque tiene autointersecciones y las formas 2, 3 y 7 son cuadriláteros porque son polígonos de cuatro lados”.
Actividad 3. Demuestra que la suma de los ángulos de un triángulo es 180º.
Respuesta nivel 2: Dibujar un triángulo, medir los ángulos y comprobar si suman 180º. Se puede distinguir entre nivel 2 bajo y nivel 2 alto, según consideren un solo triángulo o varios triángulos.
Respuesta nivel 3: Se muestra para un caso y se trata de generalizar.
Respuesta nivel 4: Se enfoca desde la generalidad.
Actividad 4. En la circunferencia dada, dibuja los diámetros AC y BD y une los extremos de los diámetros por orden para formar el cuadrilátero ABCD. ¿Qué tipo de cuadrilátero se forma? Demuestra matemáticamente que la figura que resulta es la que has dicho.
Respuesta nivel 1: No conoce las...
Similar Free PDFs

Tema II Geometría - Lecture notes 2
- 19 Pages

Tema 2 - Lecture notes 2
- 12 Pages

Unidad II - Lecture notes 2
- 14 Pages

Anatomía II Tema 2
- 3 Pages

CHI456 Lecture Notes II
- 26 Pages

Biochem II EXAM 2 Lecture Notes
- 4 Pages

Tema 2 FCE 2o - Lecture notes 12
- 1 Pages

Practica tema 2 Penal II
- 2 Pages
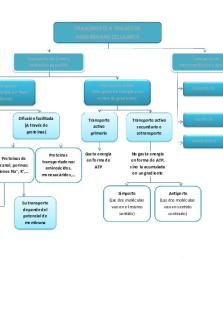
Mapa conceptual Tema 2(II)
- 1 Pages

Tema 2. Fisiología II (BN)
- 22 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu





