Método grafico Investigación de operaciones PDF

| Title | Método grafico Investigación de operaciones |
|---|---|
| Author | Gabriela Antonio |
| Course | Metodologia de la investigacion |
| Institution | Benemérita Universidad Autónoma de Puebla |
| Pages | 20 |
| File Size | 1.4 MB |
| File Type | |
| Total Downloads | 83 |
| Total Views | 119 |
Summary
Problemas resueltos...
Description
BENEMÉRITA UNIVERSIDAD AUTÓNOMA DE PUEBLA FACULTAD DE INGENIERÍA QUÍMICA
Colegio de Ingeniera Ambiental
Investigación de operaciones Facilitador: José Lucio Palacios Arias
TAREA 01 Soluciones graficas Gabriela Guadalupe Antonio Torres 201837558
Primavera 2021
Ejercicio 1. En una granja de pollos se da una dieta, para engordar, con una composición mínima de 15 unidades de una sustancia A y otras 15 de una sustancia B. En el mercado sólo se encuentra dos clases de compuestos: el tipo X con una composición de una unidad de A y 5 de B, y el otro tipo, Y, con una composición de cinco unidades de A y una de B. El precio del tipo X es de 10 euros y del tipo Y es de 30 euros. Construya el modelo de programación lineal que represente al problema. Solución: Incógnitas: x=unidades de sustancia A y=unidades de sustancia B Función objetivo: Z=10x+30y Restricciones: Sustancia A X Y
1 5 15
Sustancia B 5 1 15 x + 5y ≥ 15 5x + y ≥ 15 x ≥0 y≥0
Igualdad la función objetivo a 0 10x+30y-Z=0 Region factible: Para obtener los puntos Punto A: (0,3) x + 5y =15
x=0 → y=15/5→ y=3 Punto B: (15,0) x + 5y =15
y=0 → x=15 Punto C: (0,15) 5x + y =15
x=0 → y=15 Punto D: (3,0) 5x + y =15
y=0 → x=15/5→ x=3
Precio 10 30
Punto Optimo (x + 5y-15 =0) *5 (5x + y -15 =0)*(-1)
5x+25y-75=0 -5x-y+15=0 24y-60=0 24y=60
Realizamos nuestro sistema de ecuaciones
y=2.5 (x + 5y-15 =0) *(1) (5x + y -15 =0)*(-5)
X+5y-15=0 -25x-5y+75=0 -24x+60 X=2.5 Intersección (2.5,2.5) Sustituimos en la función objetivo
(0,15)
10(0)+30(15)=450 (15,0) 10(15)+30(0)=150 (2.5,2.5) 10(2.5)+30(2.5)=100 Valor mínimo Conclusión: Podemos concluir que el costo mínimo es de 100 euros en los cuales se obtienen de 2.5 unidades de alimento del compuesto A y 2.5 unidades de alimento del compuesto B.
Utilizando Tora
Ejercicio 2. Un establecimiento de prendas deportivas tiene almacenados 1600 bañadores, 1000 gafas de baño y 800 gorros de baño. Se quiere incentivar la compra de estos productos mediante la oferta de dos tipos de lotes: el lote A, que produce un beneficio de 8 euros, formado por un bañador, un gorro y unas gafas, y el lote B que produce un beneficio de 10 euros y está formado por dos bañadores y unas gafas. Sabiendo que la publicidad de esta oferta tendrá un costo de 1500 euros a deducir de los beneficios. Construya el modelo matemático que represente al problema Solución: Incógnitas: x= Nuero de lotes de A y= Numero de lotes B Restricciones: x y total
Bañadores 1 2 1600
x + 2y ≤ 1600 x + y ≤ 1000 x ≤ 800 x≥0 y≥0 Función objetivo: Z= 8x+10y-1500 Región factible: Punto A: (0,800) x+2y=1600 x = 0→y=1600/2=800 Punto B: (400,600) x+y=1000 (x+2y=1600) Resolvemos sistema por suma x+y=1000 -x-2y=-1600 -y=-600→y=600 X=400 Punto C: (800,200) x+y=1000 x=800 y=1000-800 →y=200
Gafas de baño 1 1 1000
Gorros 1 0 800
Costo 8 10
Punto D: (400,600) X=800 Y=0 Graficamos los puntos
Sustituimos los valores de cada punto en la función objetivo x y A 0 800 B 400 600 C 800 200 D 800 0
f(x,y)=8x+10y-1500 6500 7700 6900 4900
Conclusión: El máximo beneficio se obtiene vendiendo 400 lotes de tipo A y 600 lotes de tipo B, obteniéndose un beneficio máximo de 7700 euros.
Utilizando Tora
Ejercicio 3. Una empresa de instalaciones dispone de 195 kg de cobre, 20 kg de titanio y 14 kg de aluminio. Para fabricar 100 metros de cable de tipo A se necesitan 10 kg de cobre, 2 de titanio y 1 de aluminio, mientras que para fabricar 100 metros de cable de tipo B se necesitan 15 kg de cobre, 1 de titanio y 1 de aluminio. El beneficio que se obtiene por 100 metros de cable de tipo A es de 1500 euros, y por 100 metros de cable de tipo B, 1000 euros. Construya el modelo matemático que represente al problema. Solución: Incógnitas: x= m de cable tipo A y= m de cable tipo B x y Total
Cobre 10 15 195
Titanio 2 1 20
Restricciones: 10x + 15y ≤ 195→2x+3y≤ 39 2x + y ≤20 x + y ≤ 14 x≥0 y≥0 Función objetivo: z= 1500x+1000y Resolvemos los sistemas de ecuaciones para obtener los puntos Punto A: (0,13) 10x + 15y =195 X=0 Y=195/15→y=13 Punto B: (3,11) 2x+3y=39 -2*(X+y=14) -2y=-28→y=11 X=14-11→x=3 Punto C: (6,8) 2x+y=20 -1*(x+y=14) X=6 Y=14-6→y=8
Aluminio 1 1 14
Punto D: (10,0) 2x+y=20 Y=0 X=20/2→x=10
Sustituimos los valores de cada punto en la función objetivo A B C D
x 0 3 6 10
y 13 11 8 0
f(x,y)=1500x+1100y 14300 16600 17000 15000
Conclusión: El beneficio máximo, que es de 17000 euros, se obtiene en el punto C(6, 8). Es decir, para obtener el beneficio máximo será necesario fabricar 600 metros de cable del tipo A y 800 metros de cable tipo B
Utilizando Tora
Ejercicio 4: Una compañía posee dos minas: la mina A produce cada día 1 tonelada de hierro de alta calidad, 3 toneladas de calidad media y 5 de baja calidad. La mina B produce cada día 2 toneladas de cada una de las tres calidades. La compañía necesita al menos 80 toneladas de mineral de alta calidad, 160 toneladas de calidad media y 200 de baja calidad. Sabiendo que el costo diario de la operación es de 2000 euros en cada mina ¿cuántos días debe trabajar cada mina para que el costo sea mínimo? Resuelva el problema por el método gráfico. Solución: Variables: X= número de días trabajados en la mina A Y= número de días trabajados en la mina B
Mina A (x días) Mina B (y días)
Calidad alta
Calidad media
Calidad baja
1x 2y 80
3x 2y 160
5x 2y 200
Función objetivo: z = 2000 x + 2000 y Restricciones x + 2y ≥ 80 3x + 2y ≥160 5x + 2y ≥200 x≥0 y≥0 Resolvemos los sistemas de ecuaciones para obtener los puntos Punto A: (0,100) 5x+2y=200 X=0 y=200/2→y=100 Punto B: (40,20) -1*(X+2y=80) 3x+2y=160 2x=80→x=40 Y=(80-40)/2→y=20 Punto C: (20,50) -1*(3x+2y=160) 5x+2y=200 x=40/2→x=20
Costo diario euros 2000 x 2000 y
y=(200-100)/2 y=50 Punto D: (80,0) x + 2y =80 y=0 x=80
Sustituimos los valores de cada punto en la función objetivo A B C D
x 0 20 40 80
y 100 50 20 0
z = 2000 x + 2000 y 200000 140000 120000 160000
Conclusión: Para que el costo sea mínimo la mina A tiene que trabajar 40 días y la mina B 20 días reduciendo asi el costo a 120000 Euros.
Utilizando Tora
Ejercicio 5: Una empresa de transportes tiene dos tipos de camiones, los del tipo A con un espacio refrigerado de 20 m3 y un espacio no refrigerado de 40 m3. Los del tipo B, con igual cubicaje total, al 50 % de refrigerado y no refrigerado. La contratan para el transporte de 3.000 m3 de producto que necesita refrigeración y 4.000 m3 de otro que no la necesita. El costo por kilómetro de un camión del tipo Aes de 30 y el B de 40. ¿Cuántos camiones de cada tipo ha de utilizar para que el costo total sea mínimo? Resuelva el problema por el método gráfico. Solución: Variables: x = número de camiones de tipo A y = número de camiones de tipo B
Refrigerado No refrigerado
X 20 40
Y 30 30
Función objetivo: Z= 30x + 40y
Restricciones: 20x+30y≥3000 40x+30y≥4000 x≥0 y≥0
Resolvemos nuestro sistema de ecuaciones para obtener los puntos Punto A: (0,400/3) 40x+30y≥4000 X=0 Y=4000/3 Punto B: (150, 0) 20x+30y≥3000 Y=0 X=3000/20→X=150 Punto C: (50,67) -1*(20x+30y=3000)
Número de camiones 3000 4000
40x+30y=4000 x=100/20→x=50 40(50)+30y=4000→y=2000/30→y=66.66≈67
Graficamos:
Sustituimos los valores de cada punto en la función objetivo A B C
x 0 150 50
y 400/3 0 67
z = 30 x + 40 y 5333.332 4500 4180
Conclusión: Para obtener un beneficio por el costo mínimo se necesitan transportar 50 productos refrigerados y 67 no refrigerados con un costo total mínimo de 4180 euros.
Utilizando Tora
Ejercicio 6: Se dispone de 120 refrescos de cola con cafeína y de 180 refrescos de cola sin cafeína. Los refrescos se venden en paquetes de dos tipos. Los paquetes de tipo A contienen tres refrescos con cafeína y tres sin cafeína, y los de tipo B contienen dos con cafeína y cuatro sin cafeína. El vendedor gana 6 euros por cada paquete que venda de tipo A y 5 euros por cada uno que vende de tipo B. Calcular de forma razonada cuántos paquetes de cada tipo debe vender para maximizar los beneficios y calcular éste. Resuelva el problema por el método gráfico. Solución: Variables: X= Cantidad de paquetes tipo A a vender Y= Cantidad de paquetes tipo B a vender X Y
Con cafeína 3 2 120
Sin cafeína 3 4 180
Función objetivo: Z=6x+5y Restricciones 3x+2y≤120 3x+4y≤180 x≥ 0 y≥ 0 Resolvemos el sistema de ecuaciones para obtener los puntos Punto A: (40,0) 3x+2=120 Y=0 X=120/3→x=40 Punto B: (0,45) 3x+4y=180 X=0 Y=180/3→Y=45
Ganancia por paquete 6 5
Punto C: (20,30)
-1*(3x+2y=120) 3x+4y=180
y=60/2→y=30 3x=120-60→x=60/3→x=20 Graficamos nuestros puntos
Punto A B C
X 40 0 20
Y 0 45 30
Z=6X+5Y 240 225 270
Conclusión: Para maximizar los beneficios debe vender 20 paquetes del tipo A y 30 del tipo B. Con estas ventas obtendrá un beneficio de 270 €.
Utilizando Tora...
Similar Free PDFs
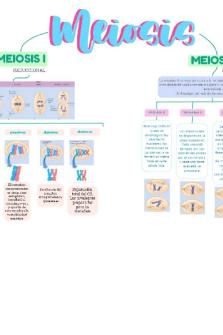
ORGANIZADOR GRAFICO DE MEIOSIS
- 1 Pages

Informe de grafico - estadistica
- 14 Pages

Grafico de resistencia
- 5 Pages

Organizador Grafico
- 3 Pages

Periodismo grafico
- 12 Pages

Organizador grafico
- 3 Pages

Organizador Grafico
- 3 Pages

Atlas Grafico DE Sistema Urinario
- 72 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu







