Przykladowe zadania z rozwiązaniami z statystyki PDF

| Title | Przykladowe zadania z rozwiązaniami z statystyki |
|---|---|
| Author | Jan Kowalski |
| Course | Statystyka matematyczna I |
| Institution | Szkola Glówna Handlowa w Warszawie |
| Pages | 8 |
| File Size | 279 KB |
| File Type | |
| Total Downloads | 35 |
| Total Views | 138 |
Summary
Download Przykladowe zadania z rozwiązaniami z statystyki PDF
Description
Zadanie 1. Obserwując liczbę awarii w sieci wodno-kanalizacyjnej w ciągu 100 dni w pewnym rejonie miasta otrzymano dane: Dzienna liczba awarii
0
1
2
3
4
Liczba dni
13
32
27
18
10
a) Na poziomie ufności 1 - =0,9 oszacować metodą przedziałową średnią dzienną liczbę awarii w l losowo wybranym dniu. b) Na poziomie ufności 1 - =0,95 oszacować metodą przedziałową wariancję dziennej liczby awarii w sieci wodno kanalizacyjnej. a) Na poziomie istotności 0,05 zweryfikować hipotezę, że średnia dzienna liczba awarii w sieci wodno-kanalizacyjnej jest równa 1,5.
Ad a). Elementem populacji generalnej jest dowolny dzień który był, jest , będzie. Cechą dla elementu populacji generalnej jest liczba awarii sieci wodno-kanalizacyjnej w przeciągu dnia w pewnym rejonie miasta. Z treści zadania wynika, że mamy dużą próbę - n=100>30 przedstawioną za pomocą szeregu rozdzielczego. Z modeli na przedziały ufności dla wartości oczekiwanej a więc średniej mamy, że założenia modelu spełnione są w modelu III, w którym cecha może mieć dowolny rozkład i wielkość próby powinna być duża ( n>30).
U Wtedy statystyka określona wzorem
X m n S ma rozkład normalny standaryzowany (w
1 P (U u ) P (
S S X m m X u n u ) P ( X u ) S n n
przybliżeniu). Wychodząc z otrzymujemy wzór na przedział ufności . W pliku na mojej stronie internetowej o nazwie Wzory estymacja.doc można znaleźć wszystkie was obowiązujące modele na przedziały ufności i wszystkie podstawowe informacje potrzebne do wyznaczenia przedziału. Aby policzyć przedział ufności zgodnie z wzorem
x u
s s m x u n n
należy wyznaczyć
wartości statystyki X i S w próbie które równają się średniej arytmetycznej x i odchyleniu standardowemu s w próbie przedstawionej za pomocą szeregu rozdzielczego. Ponadto z tablic rozkładu normalnego należy wyznaczyć kwanty u . Dane z zadania należy przedstawić jak poniżej i obliczyć te podstawowe parametry zgodnie z schematem. Cecha w populacji jest typu skokowego i przyjmuje tylko wartości całkowite. Wartości cech są środkami przedziałów klasowych.
dzienna liczba awarii
liczba dni
składniki
składniki
xi
ni
xi ni
(xi x )2 ni
0 1
13 32
0 32
42,12 20,48
2
27
54
1,08
54
25,92
40
48,40
3 4
18 10 n 1
180 138
180 138 x 1,8 s2 1,38 s s 2 1,38 1,174734 100 100 Ponieważ 1 0,9 0,1 Z tablicy rozkładu normalnego zatytułowanego P( U u ) P( U u ) 1 zamieszczonego w pliku o nazwie tablice Wszystkie potrzebne podstawowe3.doc wyznaczamy u u0,1 1,645 . kwantyle w różnych modelach można znaleźć w tym pliku. Ostatecznie 1,174734 1,174734 1,8 1,645 m 1,8 1,645 1,6 m 1,99 . Ten 100 100 przedział pokrywa z prawdopodobieństwem 1 0,9 teoretyczną średnią liczbę awarii w przeciągu dnia w sieci wodno- kanalizacyjnej w pewnym rejonie miasta.
Ad b). Szukając model przedziału ufności w tym samym pliku tylko dla wariancji i odchylenia standardowego wybieramy z tych samych powodów model II. Model I dotyczy małej próby i cecha powinna mieć rozkład normalny. Ponieważ 1 0,95 0,05 Wzór ma postać
s 2n 2 n 1 u
s 2n 2n 1 u
Ponieważ statystyka do wyznaczenia tego
przedziału miała rozkład normalny to z tej samej tablicy wyznaczamy u u0 ,05 1,96 . 1,174734 2 100
2 100 1 1,96 1,0342 2 1,3682
1,174734 2 100 2 100 1 1,96
1,034 1,368 1,069 2 1,87
Te przedziały z prawdopodobieństwem 1 0,95 pokrywają odpowiednio teoretyczne odchylenie standardowe i wariancje dziennej liczby awarii w sieci wodno- kanalizacyjnej w pewnym rejonie miasta.
Ad c). Zgodnie z treścią zadania stawiamy hipotezę, że średnia liczbę awarii w przeciągu dnia w sieci wodno- kanalizacyjnej w pewnym rejonie miasta jest równa 1,5 tzn. H 0 : m 1,5 . Na przykład do tej pory po pewnych badaniach tak się uważało. Na podstawie uzyskanej próby należy sprawdzić czy to jest dalej zdanie prawdziwe. Formułujemy hipotezę alternatywną która będzie prawdziwa po odrzuceniu hipotezy zerowej. W naszym przypadku hipoteza alternatywna będzie postaci H1 : m 1,5 tzn. , że średnia liczbę awarii w przeciągu dnia jest inna niż 1,5.
Ustalamy poziom istotności na podstawie którego będziemy weryfikować hipotezę. Te trzy elementy ustalany na podstawie treści zadania. Następnie znajdujemy statystykę za pomocą której będziemy weryfikować hipotezę przy założeniu prawdziwości hipotezy zerowej i innych nam znanych informacji. W praktyce wybieramy model do weryfikowania, w którym są spełnione założeń modelu, w którym podany jest wzór statystyki testowej i jej rozkład prawdopodobieństwa. Wszystkie modele do weryfikowania was obowiązujące są podane w pliku na mojej stronie internetowej w pliku o nazwie Weryfikacja hipotez wzory z m.doc. Postępujemy zgodnie z schematem:
0o o
1
o
2
3o
H 0 : m 1,5 0,05
H1 : m 1,5 X m0 n ~ N (0,1) tzn. wybraliśmy model III z grupy modeli do weryfikowania U S
hipotez dla wartości średniej. Ponieważ mamy dużą próbę i cecha może mieć rozkład dowolny. W pozostałych modelach założenia nie są spełnione. o Następnie obliczamy wartość statystyki z uzyskanej próby. 4 1,8 1,5 uo 100 2,55377 1,174734
Wyznaczamy obszar krytyczny czyli zbiór wartości statystyki testowej K 5o przejmujący te wartości z prawdopodobieństwem małym. W naszym przypadku z prawdopodobieństwem 0,05 tzn. P( u0 K ) . Z informacji z modelu wynika, że dla hipotezy alternatywnej pierwszej, obszar ten ma wzór K = (-; -u) (u; + ) . Ponieważ statystyka testowa ma rozkład normalny N (0,1) to z tych samych tablic jak w powyższych punktach wyznaczamy u u0 ,05 1,96 a więc zbiór krytyczny ma postać K ( ; 1,96) (1,96 ; ) o Ponieważ wartość statystyki uo 2,55377 należy do obszaru krytycznego 6 K ( ; 1,96) (1,96 ; ) tzn. u o K to hipotezę zerową odrzucamy na korzyść hipotezy alternatywnej i twierdzimy z prawdopodobieństwem przynajmniej 0,95, że hipoteza alternatywna jest prawdziwa. A więc twierdzimy z prawdopodobieństwem przynajmniej 0,95, że średnia teoretyczna liczba awarii w przeciągu dnia w sieci wodno-kanalizacyjnej w pewnym rejonie miasta jest inna niż 1,5. Z tym prawdopodobieństwem możemy uważać, że coś się zmieniło w stosunku np. co do tej pory było. Błąd w takim rozumowaniu tzn. , że hipoteza zerowa jest prawdziwa a przyjmujemy hipotezę alternatywną występuje z prawdopodobieństwem 0,05 . Jest to błąd pierwszego rodzaju
Zadanie 2 Badając zanieczyszczenie zbiornika wodnego w losowo wybranym czasie dokonano 100 pomiarów i z otrzymanych wyników utworzono szereg rozdzielczy: Zanieczyszczenie w promilach liczba wyników pomiarów w przedziale
0-4
4-8
8 - 12
12 - 16
16 - 20
8
18
27
35
12
a) Na poziomie ufności 1 - =0,9 oszacować metodą przedziałową średnie zanieczyszczenie zbiornika wodnego w losowo wybranym czasie. b) Na poziomie ufności 1 - =0,95 oszacować metodą przedziałową wariancję zanieczyszczenie zbiornika wodnego w losowo wybranym czasie. a) Na poziomie istotności a = 0,05 zweryfikować hipotezę, że średnie zanieczyszczenie zbiornika wodnego jest równe 10,5 promila. Jest to zadanie analogiczne do zadania poprzedniego i należy wyznaczyć te same zagadnienia. Elementem populacji generalnej jest losowo wybrany czas a cechą elementu populacji jest zanieczyszczenie zbiornika wodnego w losowo wybranym czasie. Istotną różnicą jest typ cechy. W naszym zadaniu cecha jest typu ciągłego i może przyjmować wszystkie wartości z określonego przedziału. Dlatego przedziały klasowe są postaci ai ;bi ) i 1,2, , , , k ai bi i do obliczenia podstawowych parametrów należy znaleźć środki przedziałów klasowych. W poprzednim zadaniu cecha elementu była typu skokowego i wartości cechy tworzyły środki przedziałów. Pozostałe elementy i próba jest analogiczna jak w poprzednim zadaniu a więc modele za pomocą których będziemy wyznaczać analogiczne zagadnienia są takie same.
Ad a). Z modelu III dla przedziałów ufności dla wartości oczekiwanej w którym spełnione są założenia modelu mamy wzór na przedział ufności x u
s n
m x u
s n.
Obliczając podstawowe parametry występujące w wzorze otrzymamy: Zanieczyszczeni ew promila ch
liczba
środki
pomiarów
składniki
przedział
xi (a i bi ) / 2
ai
bi
ni
0
4
8
2
4 8
8 12
18 27
12 16
16 20
35 12 n 100
składniki
(xi x )2 ni
xi ni
16
648,00
6 10
108 270
450,00 27,00
14 18
490 216
315,00 588,00
1100 2028
1100 2028 x 11 s2 20,28 s s 2 20,28 4,5 100 100 Ponieważ 1 0,9 0,1 i z tablic rozkładu normalnego standaryzowanego zatytułowanego P( U u ) P( U u ) 1 odczytujemy u u0,1 1,645 . Stąd 4,5 4,5 11 1,645 m 11 1,645 10, 259 m 11,741 Ten przedział pokrywa 100 100 z prawdopodobieństwem 1 0,9 teoretyczne średnie zanieczyszczenie zbiornika wodnego w losowo wybranym czasie.
Ad b). Z modelu II dla przedziałów ufności dla wariancji i odchylenia standardowego w którym spełnione są założenia modelu mamy wzór na przedział ufności
s 2n 2 n 1 u
s 2n 2n 1 u
Ponieważ 1 0,95 0,05 i z tablic rozkładu normalnego standaryzowanego zatytułowanego P( U u ) P( U u ) 1
odczytujemy u u0,05 1,96 . Stąd 4,5 2 100 2 100 1 1,96
4,5 2 100 2 100 1 1,96 1 0,95
3,96 5,24
Ten przedział pokrywa
teoretyczne odchylenie prawdopodobieństwem zanieczyszczenie zbiornika wodnego w losowo wybranym czasie.
z
standardowe
Ad c). Postępujemy zgodnie z schematem: 0o H 0 : m 10 ,5 tzn. średnie zanieczyszczenie wynosi 10,5 promil o 1 0,05
2o
H1 : m 10,5
tzn. średnie zanieczyszczenie jest inne niż
10,5
promila
3o U
X m0 S
n ~ N (0,1) tzn. wybraliśmy model III z grupy modeli do weryfikowania
hipotez dla wartości średniej. Ponieważ mamy dużą próbę i cecha może mieć rozkład dowolny. W pozostałych modelach założenia nie są spełnione. o 4 Następnie obliczamy wartość statystyki z uzyskanej próby. uo
11 10,5 100 1,11 4,5
Z informacji w modelu wynika, że dla hipotezy alternatywnej pierwszej, 5o obszar ten ma wzór K = (-; -u) (u; + ) . Ponieważ statystyka testowa ma rozkład normalny N (0,1) to z tych samych tablic jak w powyższych punktach wyznaczamy u u0 ,05 1,96 a więc zbiór krytyczny ma postać K ( ; 1,96) (1,96 ; ) o Ponieważ wartość statystyki uo 1,11 nie należy do obszaru krytycznego 6 K ( ; 1,96) (1,96 ; ) tzn. u o K to twierdzimy, że nie ma podstaw do odrzucenia hipotezy zerowej i przyjąć hipotezę alternatywną . A więc nie ma podstaw do twierdzenia, że średnie zanieczyszczenie zbiornika wodnego jest inne niż 10,5 promila. W praktyce hipotezę zerową przyjmuje się za prawdziwą np. w przypadku gdy do tej pory uważało się ją za prawdziwą.
Błąd w takim rozumowaniu tzn. , że hipoteza alternatywna jest prawdziwa a przyjmujemy hipotezę zerową występuje z prawdopodobieństwem małym ale trudnym do oszacowania. Jest to błąd drugiego rodzaju..
Zadanie 3. Zbadano dwie partie próbek 100 gramowych wątroby ze względu na zawartość węglowodanów. Zawartości węglowodanów dla I partii próbek (w g) były następujący: 15 ; 17 ; 16 ; 17 ; 18,5 ; 18 ; 17,5. Dla II partii liczącej n = 10 próbek średnia zawartość węglowodanów wynosi x = 15,5 g i odchylenie standardowe s = 1,1 g. a) Na poziomie ufności 1 - =0,9 oszacować metodą przedziałową średnią zawartość węglowodanów w próbkach 100 gramowych wątroby I partii b) Na poziomie ufności 1 - =0,95 oszacować metodą przedziałową wariancję zawartości węglowodanów w próbkach 100 gramowych wątroby I partii. c) Na poziomie istotności = 0,05 zweryfikować hipotezę, że badane partie próbek pochodzą z populacji generalnych o tej samej średniej zawartości węglowodanów .
Rozwiązanie Ad a). Z modeli na przedziały ufności dla wartości oczekiwanej a więc średniej mamy, że założenia modelu mogą być spełnione tylko w modelu II, w którym cecha powinna mieć rozkład normalny N ( m, ) . W modelu I nie znamy teoretycznego odchylenia standardowego cechy. W modelu III próba powinna być duża (n>30) . W zadaniu występuje n=7. Założenie, że X ~ N (m , ) jest do przyjęcia gdyż takie cechy przyrodnicze w większości tą własność mają. Istnieje możliwość zweryfikowania tej hipotezy i zakładamy, że ona została zweryfikowana. Wtedy statystyka X m n 1 ma rozkład t – Studenta o n-1 stopniach swobody. t S Wychodząc z prawdopodobieństwa X m S S 1 P t t, n 1 P n 1 t , n 1 P X t, n 1 m X t , n 1 S 1 n n 1 s s m x t , n 1 A stąd wzór na przedział x t , n 1 Stąd trzeba policzyć n1 n1 podstawowe parametry próby i z tablic rozkładu t – studenta odczytać kwantyl t , n 1 .
xi
( xi x ) 2
15 17 16 17 18,5 18 17,5
4 0 1 0 2,25 1 0,25
119 8,5 119 x 17 7
s2
8,5 1,214 7
s s 2 1,214 1,102
1 0,9 0,1 . Z tablic rozkładu t - Studenta zatytułowanego P( t t , n 1 ) P( t t , n 1 ) 1 odczytujemy t ,n 1 t 0 ,1;6 1,943 . Stopnie
swobody występują w pierwszej kolumnie a wartości w wierszu na górze. Stąd 1,102 1,102 m 17 1,943 17 1,943 16,126 m 17,874 Ten przedział 7 1 7 1 pokrywa z prawdopodobieństwem 1 0,9 średnią teoretyczną zawartości węglowodanów w próbkach 100 gramowych wątroby I partii
Rozwiązanie Ad b). Z modelu I dla przedziałów ufności dla wariancji i odchylenia standardowego w którym spełnione są założenia modelu mamy wzór na przedział ufności ns 2 ns 2 P 2 σ2 2 1 α χ α χ α,n 1 1 ,n 1 2 2 2 2 gdzie ,n 1 , 1 2
2
,n 1
są wartościami zmiennej
2
wyznaczonymi z tablicy rozkładu
2
z
n - 1 stopniami swobody . Model II nie możemy stosować ponieważ mamy próbę małą.
2
, n 1 2
20, 025, 6 14,449
2 1
2
,n 1
02,975,6 1, 237 . Stopnie swobody rozkładu 2
występują w pierwszej kolumnie a wartości 7 1,214 7 1,214 2 14,449 1,237
w wierszu na górze.
0,5883 2 4,3747
0,5883
4,3747
0,767 2,092
Te przedziały z prawdopodobieństwem 1 0,95 pokrywają odpowiednio teoretyczne wariancję i odchylenie standardowe zawartości węglowodanów w próbkach 100 gramowych wątroby I partii.
Rozwiązanie Ad c). Zgodnie z treścią zadania stawiamy hipotezę, że średnie zawartości węglowodanów w próbkach 100 gramowych wątroby w obu partiach są jednakowe tzn. stawiamy hipotezę zerową H 0 : m1 m2 . Mamy dwie populacje generalne związane z różnymi partiami próbek 100 gramowych wątroby. Próby w populacjach generalnych mają obliczone parametry x1 17 s1 1,102 I partia : n1 7 x2 15,5 s2 1,1 II partia : n2 10 Indeksy przy podstawowych parametrach dotyczą numeru populacji a z tym związanych numeru próby. Aby odpowiedzieć na postawione pytanie wybieramy hipotezę alternatywną pierwszą tzn. H1 : m1 m2 . Do weryfikacji hipotezy wybieramy model II spośród modeli na testy istotności dla dwóch średnich. W modelu I nie znamy teoretycznych odchylenia standardowe 1 i 2 a w modelu III próby są duże. W modelu II cechy powinny mieć rozkład normalny co w tym wypadku jak wyjaśniłem w punkcie a). jest prawdziwe. Ponadto powinno 1 2 co można sprawdzić za pomocą testu Snedecora. Dalej postępujemy zgodnie z schematem:
0 o H 0 : m1 m2
tzn. średnie zawartości węglowodanów są takie same
1o 0,05
2o H1 : m1 m2
30 t
tzn. średnie z zawartości węglowodanów są różne
X1 X 2 n S n 2S 1 1 n1 n2 2 n1 n2 2 1 1
2 2
statystyka t Studenta o n 1 n 2 2 stopniach swobody
tzn. wybraliśmy model II z grupy modeli testów istotności dla dwóch średnich. Następnie obliczamy wartość statystyki z uzyskanej próby. 4 17 15,5 t0 2,5975 7 1,214 10 1,12 1 1 7 10 2 7 10 o Z informacji w modelu wynika, że dla hipotezy alternatywnej pierwszej, 5 obszar krytyczny ma Ponieważ statystyka testowa ma rozkład t – Studenta wzór K = (-; -t,n1+n2-2) (t,n1+n2-2; + ) z tablic tego rozkładu odczytujemy t ;n1n 2 2 t 0,05;15 2,131 a więc zbiór krytyczny ma postać K ( ; 2,131) (2,131 ; ) o Ponieważ wartość statystyki t o 2,5975 należy do obszaru krytycznego 6 K ( ; 2,131) (2,131; ) tzn. to K to hipotezę zerową odrzucamy na korzyść hipotezy alternatywnej i twierdzimy z prawdopodobieństwem przynajmniej 0,95, że hipoteza alternatywna jest prawdziwa. A więc twierdzimy z prawdopodobieństwem przynajmniej 0,95, że średnia teoretyczne zawartości węglowodanów w dwóch próbach są różne. Oznacza to, że próby pochodzą z różnych populacji. Może wystąpić błąd pierwszego rodzaju tzn. że hipoteza zerowa jest prawdziwa a przyjmujemy hipotezę alternatywną. Taki błąd występuje z prawdopodobieństwem 0,05 . o...
Similar Free PDFs

Rzutyx - Zadania z rzutów
- 11 Pages

Zadania z szeregów liczbowych.
- 3 Pages
![[PBD] Zadania z podzapytań](https://pdfedu.com/img/crop/172x258/oy9gekenx4zn.jpg)
[PBD] Zadania z podzapytań
- 4 Pages

Zadania z elektrotechniki
- 2 Pages

Zadania z granic funkcji
- 2 Pages

Z-table - Z chart
- 1 Pages

Z-tabel - Z-tabel
- 3 Pages

Z tables - Z table
- 2 Pages
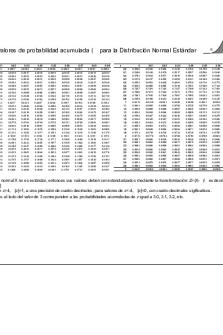
Tabla-z - Tabla Z
- 1 Pages

Notatki z wykładów z bmz
- 19 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu





