Resumen de Física II, sólo fórmulas PDF

| Title | Resumen de Física II, sólo fórmulas |
|---|---|
| Author | Mina Castillo |
| Course | Física II |
| Institution | Universidad Tecnológica Nacional |
| Pages | 47 |
| File Size | 1.8 MB |
| File Type | |
| Total Downloads | 120 |
| Total Views | 321 |
Summary
Download Resumen de Física II, sólo fórmulas PDF
Description
Resumen Física 2 (formulas)
46 pag.
TEMA 1: CARGA ELÉCTRICA - CAMPO ELÉCTRICO Partícula Masa
Protón
Neutrón −27
Electrón
−27
kg
m e = 9,11.10−31 kg
kg
m n = 1,67.10
Carga
q p = +1,60.10 −19 C
qn = 0C
qe = −1,60.10 −19 C
Carga unitaria
+1
0
-1
mp = 1,67.10
“La magnitud de la fuerza eléctrica entre dos cargas puntuales es directamente proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia”
Fe = k .
k = 9.109
q1 .q 2 r2
N.m 2 1 C2 −12 = = 8 , 84 . 10 0 C2 4π 0 N.m2
El campo eléctrico E en un punto es la fuerza por unidad de carga experimentada por una carga de prueba q 0 en ese punto.
E=
F q 1 = ⋅ 2 ⋅r° q0 4π .0 r
y
dQ
a
r
P
x
x dE Q
EP = k ⋅
Qx
(
2
)
2 3
iˆ
Donde Q es la carga total del anillo, a es el radio y x la distancia del punto al anillo de cargas. */ Estudiar la demostración /*
E=
λ
=
2 kλ r
2 π . 0 .r Donde λ es la densidad de carga lineal y r la distancia de la línea al punto. */ Estudiar la demostración /*
E=
σ 2. 0.
Donde σ es la densidad de carga superficial en el disco. Esto sólo se cumple para cuando R >> x .
E1 = E 2 =
σ 2. 0 .
E=
σ 0.
*/ Estudiar la demostración /* Sólo si las dimensiones de las láminas son grandes en comparación con la distancia entre ellas. El campo descrito es el correspondiente a cualquier punto situado entre las dos láminas. Fuera de ellas, el campo es distinto.
Una línea de campo eléctrico es una curva imaginaria dibujada a través de una región del espacio de manera que su tangente en cualquier punto tiene la dirección del vector de campo eléctrico en ese punto. Las líneas de campo nunca se intersecan.
Si el campo es uniforme, las
y uniformemente espaciadas.
¡CUIDADO!: Las líneas de campo no son trayectorias que puede seguir una partícula, ni mucho menos líneas en cuya trayectoria el campo tiene el mismo valor.
Un dipolo eléctrico es un par de cargas puntuales de igual magnitud y signo opuesto, separadas a una distancia d .
+q
p E
+
d
φ
−q En un dipolo
F
NETA
d sin φ
= 0 , pero τ ≠ 0 . Su valor es:
τ = (qE).(d sin φ ) */ Estudiar la demostración /* El producto de q por d es el momento dipolar eléctrico p :
p = qd Entonces, el momento de torsión nos queda:
τ = pE sin φ τ = p × E
x(t ) = x 0 + v 0x .t q. E Ecuaciones de Posición: donde a = 1 m y (t ) = y0 + v0 y .t + a.t 2 2 v v = x 0x Ecuaciones de Velocidad: v y = v 0 y − a.t
TEMA 2: LEY DE GAUSS q E
+
N1
θ
A
N1
El flujo eléctrico neto debido a una carga ubicada dentro de una superficie gaussiana, es independiente del área y depende sólo de la carga neta existente. Superficie gaussiana: Superficie imaginaria cerrada.
Si el campo eléctrico es uniforme, el cálculo del flujo se reduce a la ecuación:
ΦE = E ⋅ A = E. A. cos θ = E ⊥. A Pero cuando el campo eléctrico es más general, debemos tomar diferenciales e integrar. Obtenemos así la ecuación:
Φ E = E ⋅ dA = E cos θ .dA
Φ E = E ⋅ dA =
Q dentro 0
Para una superficie cerrada, que no tenga carga, el flujo es cero:
ΦE =
E ⋅ dA = 0
! ++ + + + + E = 0+ + I + + + ++
Campo interior: EI = 0
E E = k.
Campo superficial: E S = k .
q R2 E = k.
O
Campo exterior: E E = k .
q r2
q r2
r R
ΦE=
E. dA = E. cos 0º.dA = E dA
E.( 2π .r.l ) =
λ.l 0
E=
= E.( 2π .r .l ) =
λ 2 kλ 1 ⋅ = r 2 π . 0 r
Q λ .l = 0 0
q R2
Superficie Gaussiana
E
dA dA
+ + + + + + + + + + + + + + + + + +
l
E=
σ 2. 0
*/ Estudiar la demostración /*
E=
σ 0
*/ Estudiar la demostración /*
Superficie Gaussiana
Q
Qr R3 Q Campo superficial: E S = k . 2 R Q Campo exterior: E E = k . 2 r
E E = k.
Q R2
E = k.
Qr R3
O
Campo interior: E I = k .
E = k.
Q r2
R
r
El campo eléctrico en todo punto dentro de un conductor es cero, y cualquier exceso de carga en un conductor sólido se localiza por completo sobre su superficie. Si hay una carga q a nductor sin carga neta, se induce en la superficie interior una carga − q , por lo que en la superficie exterior aparece la carga q
"#$ Distribución de la carga
Punto en el campo eléctrico
Carga puntual q
Distancia r desde q
Carga q sobre superficie de esfera conductora de radio R
Fuera de la esfera ( r > R ) Dentro de la esfera (r < R )
Alambre infinito, densidad de carga
λ
Distancia r desde el alambre
Cilindro conductor infinito de radio R , carga por unidad de longitud λ
Fuera del cilindro ( r > R )
Esfera aislante sólida, carga Q distribuida uniformemente en todo el volumen.
Fuera de la esfera ( r > R )
Dentro del cilindro ( r < R )
Dentro de la esfera (r < R )
Lámina infinita de carga, con carga uniforme por unidad de área σ
Cualquier punto
Dos placas conductoras con cargas opuestas con densidades de carga superficial + σ y − σ
Cualquier punto entre las placas
q 1 ⋅ 2 4π . 0 r q 1 E= ⋅ 2 4π . 0 r E=0 1 λ ⋅ E= 2π . 0 r E=
λ 1 ⋅ 2π . 0 r E=0 1 Q E= ⋅ 2 4π . 0 r 1 Qr E= ⋅ 3 4π .0 R E=
E=
TEMA 3: POTENCIAL ELÉCTRICO % Si la fuerza es conservativa, entonces el trabajo es: b
Wa →b = F ⋅ dl = − ∆ U a
% Wa →b = Fd = q 0. E.d U = q 0 . E. y Wa →b = q 0 .E.( ya − yb ) */ Estudiar la demostración /*
%
4 π. 0 ra
Magnitud del campo eléctrico
rb
*/ Estudiar la demostración /*
σ 2.0
E=
σ 0
U=
1 ⋅ q .q 0 r 4 π . 0
*/ Estudiar la demostración /* ¡CUIDADO!: No confundir con la fórmula para la fuerza eléctrica, ésta lleva r en el denominador, no r 2
% # U=
q0
qi
4π . 0
r i
i
# U=
q i.q j 1 4π . 0 i< j rij
¡CUIDADO!: Para no repetir pares de cargas, se toma en la sumatoria sólo los i < j .
& El potencial eléctrico es la energía potencial, por unidad de carga.
V=
U q0
U = q0 .V
Vab = (Va − Vb ) =
Wa →b ∆U =− q0 q0
*/ Estudiar la demostración /*
& V=
q.q q U 1 1 ⋅ = ⋅ 0 V= q 0 4π . 0 r .q 0 4π .0 r
&# =
1
qi
&# V =
dq 1 ⋅ r 4π .0
Luego, reemplazo dq por la distribución de carga multiplicando a la dimensión, dependiendo de la geometría del problema. dq = λ .dl , o dq = σ .dA , o dq = ρ .dV
b
a
Vab = a E .dl o Vab = − b E .dl */ Estudiar la demostración /*
& ++ + + + + + + + ++ ++
E
E = k.
q R2
Potencial interior y superficial:
E = k.
q r2
VI = k. r
q V = k. R V = k.
O
R
q (constante) R
Potencial exterior: V = k.
q r
V
q r
V = k.
q r r
O
*/ Estudiar la demostración /*
& Vab = E .d
σ=
0 .V ab d ación /*
¡CUIDADO!: Ésta fórmula sirve sólo para los casos de geometría plana. En cilindros o esferas no funciona.
V=
r λ ⋅ ln 0 con r > r0 y con Vr = 0 r 2π . 0 0
*/ Estudiar la demostración /*
! y
r = x2 + a2 a
V =
P
x
x
Q 1 ⋅ 2 4π . 0 x +a2
*/ Estudiar la demostración /*
Q
y
a r = x2 + a2
y
P
V=
x
x
a2 + x2 + a Q 1 ⋅ ⋅ ln a2 + x2 − a 4π . 0 2a
*/ Estudiar la demostración /*
Q
−a
Se parte de la conservación de la energía, para llegar a la ecuación:
v=
2q0 (Va − Vb ) m
*/ Deducir la fórmula /*
'( Una superficie equipotencial es una superficie tridimensional sobre la cual el potencial eléctrico V es igual en todos sus puntos. Las líneas de campo y las superficies equipotenciales son siempre mutuamente perpendiculares.
Cuando todas las cargas están en reposo, la superficie de un conductor es siempre una superficie equipotencial.
∂V ˆ ∂ V ˆ ∂V +j +k E = − iˆ ∂y ∂z ∂x
E = −∇ V */ Estudiar la demostración /*
Er = −
∂V (Campo eléctrico Radial) ∂r
TEMA 4: CAPACITANCIA Y DIELÉCTRICOS Un Capacitor es un dispositivo que almacena Energía Potencial Eléctrica y Carga Eléctrica. Se construye aislando dos conductores y se carga realizando un trabajo, el cual se almacena como Energía Potencial Eléctrica. En un capacitor conectado a una fuente, la carga Q ( + Q en la placa positiva y − Q en la negativa) es directamente proporcional a la diferencia de potencialV ab aplicada. Entonces
Q ∝ V ab C =
Q , donde C es una constante llamada Capacitancia y que es propia de Vab
cada capacitor en especial. La unidad de la capacitancia es el farad (F =
C ) V
La capacitancia es una medida de la habilidad del capacitor para almacenar energía y depende solamente de la forma y el ta e colocado entre ellos.
Ahora 0 = 8,85.10−12 F
m
C = 0
A d
Capacitancia de un capacitor de placas paralelas en el vacío */ Estudiar la demostración /*
% C = 4π .0
ra .rb rb − r a
Capacitancia de un capacitor esférico en el vacío */ Estudiar la demostración /*
C=
2π . 0. L ln (ra rb )
Capacitancia de un capacitor cilíndrico en el vacío */ Estudiar la demostración /*
'& Capacitores en Serie:
C1
1 1 1 = + + ... C eq C 1 C 2
C2 */ Estudiar la demostración /* Capacitores en Paralelo:
C1
*/
C2
C eq = C1 + C2 + ... /*
! Q2 1 1 = C.V 2 = Q.V U= 2C 2 2
Energía Potencial almacenada en un Capacitor */ Estudiar la demostración /*
u=
1 0 .E 2 2
Densidad de energía eléctrica en el vacío. */ Estudiar la demostración /* También podemos calcular la Energía Potencial de un Capacitor integrando la densidad de energía:
U = u.dV donde dV es el diferencial de volumen que dependerá de la forma del capacitor.
Cuando colocamos un material dieléctrico entre las placas, aumenta la diferencia de potencial máxima posible sin que ocurra la ruptura dieléctrica y entre en conducción. Además, la carga Q se mantiene, pero el potencial V disminuye, por lo que la capacitancia C aumenta
K=
C C0
Constante Dieléctrica (adimensional) Dicha constante toma un valor 1 para el vacío, y mayor que 1 para otros materiales (a 20º C )
#
σ i = σ 1 −
1 K
Densidad de carga superficial inducida Donde σ es la densidad de carga por unidad de área de las placas yK es la constante dieléctrica del material. */ Estudiar la demostración /*
= K . 0 Permitividad del Dieléctrico La capacitancia en placas paralelas, cuando se tiene presente un dieléctrico está dada por:
C = K .C 0 = K . 0.
A d C =⋅
A d
Capacitancia de un capacitor de placas paralelas con dieléctrico
1 2 u = .E 2 Densidad de energía eléctrica en un dieléctrico
KE ⋅ dA =
Q dentro-libre 0
*/ Estudiar la demostración /*
TEMA 5: CORRIENTE Y RESISTENCIA - FUERZA ELECTROMOTRIZ I=
dQ dt
Definición de Corriente Eléctrica
[ I ] = A = Ampere = C s
) También podemos definir la corriente a través de n (concentración de partículas por unidad de volumen en m -3 ), v d (velocidad de arrastre de las partículas), A (área de la sección de conductor) y q (carga de cada partícula), de la siguiente manera:
I=
dQ = n .q .v d .A dt
*/ Estudiar la demostración /* Definimos también densidad de corriente J como la corriente que pasa por una unidad de área transversal:
I = n. q .v d A J = n.q.v d (vector) J=
* ρ=
E
[ρ] = Ω.m
Un material que obedece la Ley de Ohm razonablemente bien se conoce como conductor ohmico o lineal. Para tales materiales, a una temperatura dada, ρ es constante y no depende del valor de E .
* La resistividad de un material varía dependiendo de la temperatura. En un pequeño intervalo de temperaturas (hasta unos 100º C ), la resistividad del metal puede representarse aproximadamente por la ecuación:
ρ (T ) = ρ 0 .[1 + α (T − T0 )] donde ρ 0 es la resistividad a una temperatura T 0 y α es el coeficiente de temperatura de la resistividad.
* R=ρ
L A
[R] = Ω = Ohm = V A
En correspondencia con la resistividad, la temperatura también afecta a la resistencia en igual proporción:
R (T ) = R 0 .[1 + α (T − T 0 )] donde R 0 es la resistividad a una temperatura T 0 y α es el mismo coeficiente.
+, V = I .R A ésta expresión se la suele llamar Ley de Ohm, pero el contenido real de ésta ley es proporcionalidad directa entreV e I . Mas sólo es así si la resistencia es constante.
Para que un conductor tenga una corriente estacionaria, debe formar parte de una trayectoria que constituya un camino cerrado o circuito completo. Cuando en dos extremos de un conductor se establece una diferencia de potencial, las cargas “bajan” de un punto de mayor potencial a uno de menor, generando un movimiento de cargas y por lo tanto una corriente eléctrica. Para poder llevar las cargas nuevamente hacia el punto de un mayor potencial es necesaria una “fuerza”, a la que llamaremos Fuerza Electromotriz o fem, pero es importante tener en cuenta que la fem no es una fuerza sino una cantidad de energía por unidad de carga representada por la misma unidad que el potencial (Volt). Representaremos a la fem con el símbolo . En cualquier circuito completo con una corriente estacionaria debe haber un dispositivo que proporcione fuerza electromotriz, al que llamaremos fuente de fem.
ε
En una fuente ideal de fem
ε =V
ab
= I .R
* Las fuentes de fem reales de un circuito presentan
ε
≠ Vab , pues la carga que se mueve a través
del material de la fuente encuentra resistencia, a la que llamaremos resistencia interna de la fuente y representaremos con r , entonces:
Vab = ε − I.r (voltaje en terminales de una fuente con resistencia interna) Para una fuente real de fem, el voltaje en terminales es igual a la fem sólo si no fluye corriente por la fuente. Ahora la corriente será:
I=
ε R+r
- V Amperímetro: Siempre en serie con el circuito
A
Voltímetro: Siempre en paralelo con el circuito
% P=
dW J = V ab .I [P ] = W = Watt = dt s
(razón a la cual se entrega energía eléctrica a un elemento del circuito)
* P = Vab .I = I 2 .R =
Vab 2 R
(potencia proporcionada a un resistor) La energía se disipa en el resistor a razón de I 2.R
& P = V . I = ε .I − I 2 .r */
/*
es la razón a la cual hace trabajo sobre las cargas en movimiento cualquier agente εque.Iesté ocasionando las fuerzas no electrostáticas en la fuente. El término I 2 .r es la razón con que se disipa la energía eléctrica en la resistencia interna de la fuente.
...
Similar Free PDFs

Resumen de Derecho Mercantil II
- 62 Pages

Resumen solemne II de morfologia
- 9 Pages

Pre SLO Test Spring 2020
- 4 Pages

Excel SLO 8.3-Using Solver
- 4 Pages

Resumen de Formulas de AM II
- 6 Pages

Resumen-patologica-II
- 102 Pages

Derecho Romano II resumen
- 25 Pages

Coele II resumen definitivo
- 117 Pages

Resumen 6.1, Isabel II
- 2 Pages

Resumen Estadistica II parcial
- 15 Pages

Resumen Filosofia II
- 37 Pages
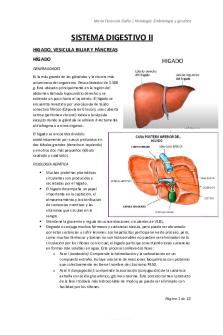
Sistema digestivo II resumen
- 13 Pages

Concilio Vaticano II resumen
- 4 Pages

Resumen Contratos II
- 46 Pages

Formulario II - Resumen Física
- 3 Pages

Resumen sistema digestivo II
- 8 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu