01 Metodo Grafico PDF

| Title | 01 Metodo Grafico |
|---|---|
| Author | Majid Arif |
| Course | Modelli e algoritmi di ottimizzazione (9 crediti) |
| Institution | Università degli Studi di Bergamo |
| Pages | 13 |
| File Size | 592.6 KB |
| File Type | |
| Total Downloads | 109 |
| Total Views | 156 |
Summary
01 Metodo Grafico...
Description
METODO GRAFICO Fra i problemi di Ricerca Operativa, hanno assunto particolare importanza quelli di Programmazione Lineare. Si è in presenza di un problema lineare quando questo si traduce in un modello matematico costituito da: a. una funzione lineare in n variabili (tutte di primo grado), detta obiettivo che normalmente esprime un costo (da minimizzare) oppure un ricavo o un guadagno (da massimizzare); b. un sistema di vincoli espressi da equazioni o disequazioni, lineari nelle n variabili (di primo grado) e sono detti vincoli tecnici o funzionali; c. un sistema di vincoli di segno, che esprimono la non-negatività delle variabili, trattandosi di grandezze economiche. Dal punto di vista matematico, si parla allora di problemi per la ricerca di massimi o minimi vincolati. Nel caso in cui le variabili decisionali sono due (x1 e x2, per esempio), si può risolvere il problema con il metodo grafico, rappresentando il modello nel piano cartesiano. I vincoli di segno limitano la ricerca delle soluzioni al primo quadrante. Dopo aver tracciato tutte le rette associate alle disequazioni ed equazioni del sistema dei vincoli, se l€intersezione derivante non è un insieme vuoto, si otterrà un poligono (o una regione illimitata) detto regione ammissibile, perché contiene tutte le coppie (x1, x2) che soddisfano le disequazioni e/o le equazioni del sistema. Ciascuna di queste coppie è detta soluzione ammissibile, mentre le coppie di valori che corrispondono ai vertici del poligono sono dette soluzioni ammissibili di base: fra esse va cercata, se esiste, la soluzione ammissibile ottima del problema. In corrispondenza di ogni vertice del poligono, infatti, si calcola il valore della funzione obiettivo, e si sceglie la coppia che rende ottima (cioè massima o minima, a seconda dei casi) la funzione stessa (è questa la conseguenza diretta del teorema fondamentale della programmazione lineare: il massimo ed il minimo di una funzione lineare di un numero qualsiasi di variabili soggetta a vincoli espressi da equazioni e/o da disequazioni lineari, se esistono, si trovano sui vertici della regione ammissibile, e non al suo interno). Nel caso particolare in cui in corrispondenza di due vertici consecutivi si ottiene lo stesso valore della funzione obiettivo, la teoria della programmazione lineare dimostra che lo stesso valore si ottiene in corrispondenza di un qualsiasi punto compreso tra i due vertici suddetti.
1 Esercitazioni di P.L.: Metodo grafico --
Esempio 1 Un reparto di un'azienda di elettrodomestici può produrre giornalmente non più di 6 lavatrici, delle quali alcune sono di un tipo A e le altre di un tipo B. Il turno di lavoro non può superare le 8 ore giornaliere; una lavatrice di tipo A richiede 2 ore di lavoro, mentre una di tipo B ne richiede una. Se una lavatrice di tipo A costa 600 euro una di tipo B 400 euro, quante lavatrici di ciascun tipo devono essere prodotte giornalmente affinché l'azienda realizzi il massimo guadagno? Nell'enunciato ci sono molte informazioni ed è un po' difficile tenerle tutte a mente e intravedere rapidamente un procedimento per risolvere il problema. E€ però importante rilevare che, una volta trovata la soluzione, l'azienda sarà in grado di programmare la produzione del reparto. Percorso risolutivo Risorse
A
B
Impieghi N° lavatrici x1 Ore di lavoro al giorno 2 €600 Profitto unitario Rendere massimo il profitto x1 = numero di lavatrici di tipo A x2 = numero di lavatrici di tipo B
Disponibilità giornaliera per ogni risorsa
x2 6 1 8 €400 ω = 600x1 + 400x2
x1 + x 2 ≤ 6 2x1 + x2 ≤ 8
Si hanno le seguenti restrizioni: • il numero complessivo delle lavatrici non può essere superiore a 6 • la durata massima del lavoro non può superare le 8 ore giornaliere • il numero di ciascuna lavatrice non può essere negativo. L'obiettivo dell'azienda è decidere quante lavatrici (di ciascun tipo) produrre giornalmente affinchè venga realizzato il massimo profitto. La funzione che esprime il guadagno dell'azienda in euro viene chiamata funzione obiettivo ed è ω = 600x1 + 400x2 Il problema consiste perciò nel trovare i valori di x1 e x2 che rendano la funzione obiettivo più grande possibile sotto le condizioni espresse dalle disequazioni lineari viste prima che, dovendo valere simultaneamente, costituiscono il seguente sistema: max 600 x1 400 x2 o max z 600 x1 400 x 2 x1 x 2 6 s.a 2 x1 x 2 8 x1 , x 2 0 Si deve ricercare il massimo di una funzione economica a 2 variabili con vincoli dati da disequazioni lineari, conviene seguire attentamente i seguenti passaggi: a) si determina il dominio dei vincoli (o regione del piano x1Ox2 delle soluzioni ammissibili) b) se il dominio dei vincoli e' un poligono si calcolano i valori della funzione data nei vertici del poligono e si tra essi il valore massimo se la funzione data si deve massimizzare, oppure il valore minimo se la funzione data si deve minimizzare. c) se il dominio dei vincoli e' illimitato si esaminano alcune linee di livello nell'interno del dominio dei vincoli per capire se esiste un punto che ottimizza la funzione economica data. Quindi, per risolvere in via geometrica un problema di programmazione lineare dobbiamo costruire un grafico. In questo grafico dobbiamo disegnare la regione ammissibile che è ricavata disegnando tutti i vincoli del nostro problema. Se l'insieme non è vuoto, tale area può essere rappresentata da un poligono, o da una poligonale illimitata, che possono eventualmente ridursi ad una semiretta, ad un segmento o ad un punto. 2 Esercitazioni di P.L.: Metodo grafico --
Le disequazioni x1 ≥ 0 e x 2 ≥ 0 (vincoli di segno) sono soddisfatte da tutti i punti che sono nel 1° quadrante le cui coordinate, x1 e x2, sono non negative
La disequazione x1 + x2 ≤ 6 è soddisfatta da tutti i p unti appartenenti al semipiano inferiore rispetto la retta x2 = - x1 + 8
La disequazione 2x1 + x2 ≤ 8 è soddisfatta da tutti i punti appartenenti al semipiano inferiore rispetto la retta x2 = -2x1 + 4
L'insieme delle soluzioni è la regione OABD ossia l'intersezione dei semipiani corrispondenti alle quattro disequazioni del sistema. Per ottenere la soluzione che assicuri il massimo guadagno, cioè la soluzione ottimale, dobbiamo cercare i punti le cui coordinate rendano massimo il valore della funzione obiettivo. Quali punti cercare? Teorema 1. Si può dimostrare in modo del tutto generale che le soluzioni ottimali di un problema di programmazione lineare sono i punti situati sul contorno, e in particolare nei vertici dell'insieme di soluzione. In un problema di programmazione lineare se l'insieme delle soluzioni ammissibili è un poligono chiuso, allora è un poligono chiuso convesso. Teorema (Weierstrass + teo. fondamentale progr. lin.) Se l'insieme delle soluzioni ammissibili è un poligono convesso, il massimo e il minimo esistono e si trovano in un vertice del poligono. Per determinare i punti estremi basta calcolare i valori della funzione obiettivo nei vertici del dominio, se questo è un poligono chiuso. Se il dominio dei vincoli è illimitato si esamina invece l'andamento delle curve di livello per determinare, se esiste, un punto che ottimizza la funzione obiettivo. Se in due vertici consecutivi la funzione obiettivo assume lo stesso valore, essa assume quello stesso valore in tutti i punti del segmento che li unisce. Nel nostro caso, alcuni di tali punti sono i punti O, A, D, B. Calcoliamo i valori della f.o. nei punti sul contorno Guadagno ω = 600x1 + 400x2 O(0; 0) ω = 0 D(4; 0) ω = 2400 C(0; 6) ω = 2400 B(2; 4) ω =1200+1600 = 2800 La soluzione ottimale è data da x1 = 2 e x2 = 4. Perciò producendo giornalmente 2 lavatrici di tipo A e 4 di tipo l'azienda realizza il massimo guadagno di 2800 euro.
3 Esercitazioni di P.L.: Metodo grafico --
Esempio 2 Risolvere con il metodo grafico il problema di programmazione lineare: min φ = 4x1 + x2 s.a 2x1 - x2 ≤ 8 x1 + 2x2 ≤ 10 5x1 + x2 ≥ 5 x1 , x 2 ≥ 0 Si rappresenta la regione ammissibile (l€insieme delle soluzioni ammissibili osservando che: Le disequazioni x1 ≥ 0 e x 2 ≥ 0 (vincoli di segno) sono soddisfatte da tutti i punti che sono nel 1° quadrante le cui coordinate, x1 e x2, sono non negative
La disequazione 2x1 - x2 ≤ 8 è soddisfatta da tutti i punti appartenenti al semipiano superiore rispetto la retta x2 = 2x1 - 8
La disequazione x1 + 2x2 ≤ 10 è soddisfatta da tutti i punti appartenenti al semipiano inferiore rispetto la retta x2 = (-1/2)x1 + 5
La disequazione 5x1 + x2 ≥ 5 è soddisfatta da tutti i punti appartenenti al semipiano superiore rispetto la retta x2 ≥ -5x1 + 5 Si disegnano le rette del fascio φ = 4x1 + x2 → x2 = - 4x1 + φ cioè dal grafico si potrà dedurre come vertice “ottimo “quello cui corrisponde il minimo valore dell€ordinata all€origine del fascio x2 = - 4x1 + φ
I vertici della regione ammissibile (tra cui vi sarà la soluzione ottima) sono i punti A (1;0), B( 4;0), C(26/5; 12/5), D(0; 5), dal grafico è evidente che il minimo valore la f.o. φ lo assume nel vertice A, come è possibile verificarlo calcolando il valore di φ in ogni vertice:
φ (A) = φ (1, 0) = 4 φ (B) = φ (4, 0) = 16 φ (C) = φ (26/5, 12/5) =116/5 φ (D) = φ (0, 5) = 5 Il valore minimo per la f.o. φ è φ (A) = 4
4 Esercitazioni di P.L.: Metodo grafico --
Esempio 3 Una industria produce un bene di consumo in due versioni, normale e super. Su ogni unità venduta l€industria ha un profitto di 1200€ per il tipo normale e di 1500€ per il tipo super. Nella produzione sono utilizzati tre tipi di macchinari, che indichiamo convenzionalmente con A, B, C, e che settimanalmente non possono essere in esercizio per un numero di ore maggiore di quello indicato nella tabella di seguito riportata; per produrre una unità di prodotto è richiesto l€utilizzo delle macchine per il tempo indicato nella stessa tabella : macchinario ore per settimana Ore di lavoro per unità di prodotto Tipo normale Tipo super A 1500 1,5 1,5 B 2000 0,8 1 C 1800 1 2 Profitto 1200 1500 L€industria vuole pianificare la produzione settimanale in modo da massimizzare il profitto conseguito. Indicando rispettivamente con x1 e x2 le quantità del bene prodotto settimanalmente nella versione normale e nella versione super, il profitto settimanale è dato dalla funzione ω = 1200x1 + 1500x2. Per non superare la capacità lavorativa delle macchine di tipo A dovrà risultare 1.5x1 + 1.5x2 ≤ 1500 e disuguaglianze analoghe valgono per le macchine di tipo B e C, per cui si ha 0.8x1 + x2 ≤ 2000, x1 + 2x2 ≤ 1800. Poichè infine deve risultare x1 ≥ 0, x2 ≥ 0, giungiamo alla formulazione del seguente problema di programmazione lineare: max ω = 1200x1 + 1500x2 o max z = 1200x1 + 1500x2 s.a. x2 = -4/5x1 + ω /1500 “fascio improprio di rette” 1.5x1 + 1.5x2 ≤ 1500 0.8x1 + x2 ≤ 2000 x1 + 2x2 ≤ 1800 x1 ≥ 0, x2 ≥ 0. Rappresentazione grafica dei vincoli e della funzione obiettivo I. x2 = - x1 + 1000 x1 x2 0 1000 1000 0 II. x2 = -4/5x1 + 2000 x1 x2 0 2000 2500 0 x1 x2 III. x2 -1/2x1 +900 0 900 1800 0 f.o. x2 = -4/5x1 x1 x2 retta di riferimento del fascio 0 0 5 -4
5 Esercitazioni di P.L.: Metodo grafico --
Vertici della regione ammissibile: (0;0), (0; 900), (200;800) e (1000;0) Dal grafico si vede che il max della f.o. è nel vertice C (200;800) intersezione delle rette (vincoli)
della regione ammissibile,
1,5x1 +1,5x2 ≤ 1500 x1 + 2x2 ≤ 1800 Soluzione ottima ω = 1440000 in x1 = 200, x2 =800, cioè vengono prodotte 200 unità del primo prodotto di tipo normale e 800 unità del secondo di tipo super. Osserviamo inoltre che il secondo vincolo non modifica la regione ammissibile “potrebbe” essere addirittura trascurato e si dice ridondante.
6 Esercitazioni di P.L.: Metodo grafico --
CASI PARTICOLARI “Soluzioni ottime alternative “ La soluzione ottimale di un problema di p-l non è necessariamente unica, questa circostanza si verifica allorché le curve di livello della funzione obiettivo sono parallele ad una delle facce del poliedro che rappresenta la funzione obiettivo. Riprendendo l€esempio precedente si supponga che il profitto per il prodotto normale sia di 1500 €, in luogo dei 1200 € originariamente ipotizzati, a parità di tutte le altre condizioni del problema. macchinario A B C
ore per settimana 1500 2000 1800 Profitto
Ore di lavoro per unità di prodotto Tipo normale Tipo super 1,5 1,5 0,8 1 1 2 1500 1500
Sotto le nuove ipotesi il problema si riformulerà come: max ω = 1500x1 + 1500x2 o max z = 1500x1 + 1500x2 s.a. x2 = - x1 + ω /1500 “fascio improprio di rette” 1.5x1 + 1.5x2 ≤ 1500 0.8x1 + x2 ≤ 2000 ridondante x1 + 2x2 ≤ 1800 x1 ≥ 0, x2 ≥ 0. Con la rappresentazione dei vincoli e della f.o. si ottiene il grafico
Una faccia della regione ammissibile (il segmento CD) è parallela alle curve di livello, e quindi tutti i mix produttivi corrispondenti ai punti di tale faccia sono soluzioni ottimali. Rimane tuttavia vero che almeno un vertice è ottimale (in questo caso i vertici ottimali sono due), e quindi l€enumerazione dei soli vertici costituisce anche in questo caso una procedura risolutiva corretta. ω (C ) = ω ( D) = 1.500.000€.
7 Esercitazioni di P.L.: Metodo grafico --
“Soluzioni degeneri” Riprendendo l€esempio 3 si supponga che per il macchinario B le ore di lavoro subiscano delle variazioni a parità di tutte le altre condizioni del problema secondo la tabella macchinario
ore per settimana
Ore di lavoro per unità di prodotto Tipo normale Tipo super A 1500 1,5 1,5 B 1200 2 1 C 1800 1 2 Profitto 1200 1500 Sotto le nuove ipotesi il problema si riformulerà come: max ω = 1200x1 + 1500x2 o s.a. 1.5x1 + 1.5x2 ≤ 1500 2x1 + x2 ≤ 1200 x1 + 2x2 ≤ 1800 x1 ≥ 0, x2 ≥ 0.
max z = 1200x1 + 1500x2 x2 = - 4/5x1 + ω /1500 “fascio improprio di rette”
Rappresentazione grafica dei vincoli e della funzione obiettivo I. x2 = - x1 + 1000 x1 x2 0 1000 1000 0 II. x2 = - 2x1 + 1200 x1 x2 0 1200 600 0 x1 x2 III. x2 -1/2x1 +900 0 900 1800 0 f.o. x2 = -4/5x1 x1 x2 retta di riferimento del fascio 0 0 50 - 40 Con la rappresentazione dei vincoli e della f.o. si ottiene il grafico
La soluzione ottima determinata corrisponde al vertice C rappresenta una soluzione degenere, in quanto in esso sono attivi tre vincoli , cioè un numero di vincoli maggiore della dimensione del problema ed è nulla una v.b. Il punto C lo si può pensare come intersezione del 1° e 2° vincolo tecnico del 1° e 3° vincolo tecnico 8 Esercitazioni di P.L.: Metodo grafico --
del 2° e 3° vincolo tecnico
“Problemi privi di soluzione ottima” Vi sono due circostanze nelle quali un problema non ammetta soluzioni ottimali : 1. non esistono soluzioni ammissibili per il problema la regione ammissibile è vuota 2. pur essendo non vuota la regione ammissibile, la funzione obiettivo risulta superiormente illimitata nel caso di un problema di massimizzazione (o inferiormente nel caso di un problema di minimizzazione)
1.”Regione ammissibile vuota” Consideriamo il problema di P.-L. max ( x1+x2) s.a -x1+2x2 ≤ -1 x1 - x2 ≤ -1 x1 , x 2 ≥ 0 La rappresentazione grafica indica che i vincoli del problema sono tra loro incompatibili, e che di conseguenza la regione ammissibile è vuota Un tale problema può presentarsi come conseguenza di errori logici nella formulazione di un modello, o più banalmente può dipendere da errori nella raccolta o inserimento dei dati del problema stesso.
9 Esercitazioni di P.L.: Metodo grafico --
2.”Funzione obiettivo illimitata” Consideriamo il problema di P.-L. max x1 + x2 s.a - x1 + x2 ≤ 3 - x1 - x2 ≤ -1 x1 - x 2 ≤ 2 x1, x2 ≥ 0
r.a. illimitata D(0,3)
C(0,1)
A(1,0
B(2,0)
La rappresentazione grafica indica che la regione ammissibile è illimitata. Le curve di livello (rette) si spostano verso l€alto e possono crescere oltre ogni limite, perciò non è possibile trovarne il valore massimo: il problema non ha soluzione ottima finita. La illimitatezza della regione ammissibile è condizione necessaria ma non sufficiente per l€illimitatezza del problema associato. Infatti se il modello fosse min ( x1 + 2x2) s.a - x1 + x2 ≤ 3 - x1 - x2 ≤ -1 x1 - x 2 ≤ 2 x1, x2 ≥ 0 allora la soluzione ottimale coinciderebbe con il vertice di coordinate (2, 0).
D(0,3) RA illimitata
C(0,1)
A(1,0)
B(2,0)
10 Esercitazioni di P.L.: Metodo grafico --
Esercizi 1 max ω = 2x1 - 4x2 s.a. -3x1 - 5x2 ≤ -15 4x1 + 9x2 ≤ 36 x 1, x2 ≥ 0 2 max ω = 3x1 + 2x2 s.a. -3x1 + 2x2 ≤ 6 - x1 + x2 ≤ 4 x1 , x 2 ≥ 0 3 min φ = -2x1 - x2/2 s.a. -6x1 - 5x2 ≥ - 30 - 4x1 - x2 ≥ -12 x1 , x 2 ≥ 0 4 min φ = 2x1 - 3x2 s.a. - x 1 - x2 ≤ 0 x2 ≤ 5 x 1, x2 ≥ 0 5 min φ = -x1 - 3x2 s.a. 2x1 + x2 ≥ 5 x1 - x2 ≤ 4 -x1+ 2x2 ≤ 4 x1 , x2 ≥ 0 6 min φ = -x1 s.a. x1 - x2 ≤ 3 2x1 + x2 ≤12 -x1+ 2x2 ≤14 x1 , x 2 ≥ 0 7 min φ = -x1 - 2x2 s.a. 4x1 - x2 ≥ 4 x1 + 2x2 ≤10 x1 - x 2 ≤ 4 x 1, x2 ≥ 0 8 min φ = -x1 + 3x2 s.a. x1 + x2 ≥ 3 -x1 + x2 ≤ 5 x1 - 2x2 ≤ 5 x 1, x2 ≥ 0 9 min φ = 2x1 + x2 s.a. x1 - 2x2 ≥- 4 2x1 + 3x2 ≤ 13 4x1 + x2 ≤ 16 x 1, x2 ≥ 0 11 Esercitazioni di P.L.: Metodo grafico --
RISOLUZIONE Esercizio 5 Risolvere con il metodo grafico il problema di programmazione lineare: min φ = -x1 - 3x2 s.a. 2x1 + x2 ≥ 5 x1 - x 2 ≤ 4 -x1+ 2x2 ≤ 4 x1 , x 2 ≥ 0 Si rappresenta la regione ammissibile (l€insieme delle soluzioni ammissibili osservando che: Le disequazioni x1 ≥ 0 e x 2 ≥ 0 (vincoli di segno) sono soddisfatte da tutti i punti che sono nel 1° quadrante le cui coordinate, x1 e x2, sono non negative La disequazione 2x1 + x2 ≥ 5→ x2 ≥ - 2x1 + 5 → semipiano superiore (≥) rispetto la retta x 2 = - 2x1 + 5
è soddisfatta da tutti i punti appartenenti al
La disequazione x1 - x2 ≤ 4 → x2 ≥ x 1 - 4 è soddisfatta da tutti i punti appartenenti al semipiano superiore (≥) rispetto la retta x2 = x1 – 4 La disequazione -x1+ 2x2 ≤ 4→ x2 ≤ (1/2)x 1 + 2 è soddisfatta da tutti i punti appartenenti al semipiano inferiore (≤) rispetto la retta x2 = (1/2)x1 + 2 Si disegnano le rette frontiere dei semipiani associati ai vincoli e si disegnano le rette del fascio improprio relativo alla f.o. φ = x1 - 3x2→ x2 = (-1/3)x1 – φ /3. Dalla espressione dela f.o. osserviamo che il minimo valore di φ corrisponde il vertice (soluzione di base) per cui passa la retta del fascio di intercetta massima, infatti min φ = max - φ I. x2 = - 2x1 + 5 II. x2 = x1 – 4
III x2 = (1/2)x1 + 2 f.o. x2 = (-1/3)x1
x 1 x2 0 5 2 1 x1 x2 0 -4 4 0 x1 x2 0 2 2 3 x1 x2 0 0 3 -1
Ne segue che la regione ammissibile è rappresentata dal quadrilatero irregolare ABCD e la f.o. dalle rette del fascio
12 Esercitazioni di P.L.: Metodo grafico --
la retta del fascio di intercetta massima è la retta per il vertice A intersezione della frontiera del 2° e 3° vincolo perciò le sue coordinate saranno determinate con la risoluzione del sistema:
x1 x2 4 x 2 x 4 2 1 A(12, 8) ed in esso la φ assume valore φ = -12 -3(8) = -36 Per una ulteriore conferma sarà possibile calcolare il valore della φ in ogni vertice della r.a. B (4, 0) e φ (B) = - 4 C (5/2, 0) e φ (C) = - 5/2 D (6/5, 13/5) e φ (D) = - 9 Perciò il valore ottimo per la f.o. φ è φ (A) = -36
13 Esercitazioni di P.L.: Metodo grafico --...
Similar Free PDFs

01 Metodo Grafico
- 13 Pages

Organizador Grafico
- 3 Pages

Periodismo grafico
- 12 Pages

Organizador grafico
- 3 Pages

Organizador Grafico
- 3 Pages

Metodo
- 7 Pages

Abecedario del grafico riassunti
- 3 Pages

Tarea #1 Organizador Grafico
- 2 Pages
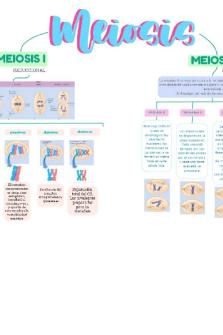
ORGANIZADOR GRAFICO DE MEIOSIS
- 1 Pages

Informe de grafico - estadistica
- 14 Pages

MÉTODO GRAFICO MCCABE THIELE
- 25 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu




