Cap 1 logaritmos - Nota: 10 PDF

| Title | Cap 1 logaritmos - Nota: 10 |
|---|---|
| Author | Alexandra Gonzalez |
| Course | Matemática Financiera |
| Institution | Universidad de Cuenca |
| Pages | 14 |
| File Size | 502.9 KB |
| File Type | |
| Total Downloads | 55 |
| Total Views | 187 |
Summary
cap libro vicente mendez ...
Description
CAPÍTULO 1
LOGARITMOS
1.1 SIMBOLOGÍA log x:
Logaritmo común o decimal
ln x:
Logaritmo natural o neperiano
e:
2.71828183
10x:
Antilogaritmo de base 10
e x:
Antilogaritmo de base e
MATEMATICAS FINANCIERAS CON EXCEL Y MATLAB
2
1.2 INTRODUCCIÓN Los logaritmos sirven, entre otras aplicaciones, para agilizar el cálculo de algunas operaciones matemáticas como la multiplicación, división, potenciación y radicación, exceptuando la suma y la resta. Si bien los cálculos manuales con logaritmos han sido sustituidos por la utilización de las calculadoras y computadores, el concepto de logaritmo y su aplicación matemática es de uso especialmente en ciertos temas. Diversas operaciones de análisis matemático no podrían ser resueltas sin la aplicación de este concepto y en algunos casos de matemáticas financieras es indispensable. 1.3 DEFINICIONES Lo primero que debe recordarse es que un logaritmo es un exponente , pero con algunas características particulares que vamos a estudiarlas a continuación. Sin embargo, debe mantenerse siempre presente que logaritmo es prácticamente sinónimo de exponente. En el caso de una ecuación exponencial de la forma b y = x en donde (b>0, b 1), la variable x se expresa en términos de un número real b y la variable y. El exponente y se denomina el logaritmo de x en base b. x b y (x>0) y log b x si y solo si 1.4 LEYES DE LOS EXPONENTES Suponiendo que "a" y "b" son números positivos; y, que "u" y "v" son números reales, las leyes aplicables a los exponentes son: 1.4.1 a u * a v a u v 1.4.2 a u / a v au v 1.4.3 ( a u )v au* v u u u 1.4.4 (ab) a * b u
au a 1.4.5 u b b Se puede expresar operaciones matemáticas con términos de este tipo, ejemplo: 122 + 245 2504 – 5403 753 * 1506 15012 / 83
suma de términos resta de términos multiplicación de términos división de términos
3
LOGARITMOS
Puede haber situaciones en que las bases de los números son las mismas, como: 1223 + 125 124 – 123 123 * 126 1214 / 123 Para la suma y resta no es posible una solución matemática directa, pero para la multiplicación y división si: 123 * 126 = 123 + 6 = 129 1214 / 123 = 1214 - 3 = 1211 De esta manera, si la base es la misma, la multiplicación de términos se resuelve con la suma de sus exponentes, mientras que la división de términos con la resta de sus exponentes. La potenciación y radicación, se resuelve con multiplicación y división de exponentes respectivamente: (124) 3 = 124* 3 = 1212 3
1212 = 1212/ 3 = 124
Términos con un misma base Suma: bu + bv Resta: bu – bv Multiplicación: bu * bv División: bu / bv Potenciación: (bu) v Radicación:
v
bu
Para resolver con los exponentes No aplica No aplica Sumar exponentes: u+v Restar exponentes: u-v Multiplicar exponentes: u*v Dividir exponentes: u/v
Los logaritmos se basan en estos conceptos matemáticos. Se puede establecer logaritmos (exponentes) de cualquier base, como el número 12 en el caso del ejemplo anterior, en donde: 124 tiene como exponente el 4, equivale a decir: 124 log12(124) = 4 que se lee, logaritmo de base 12 del número 20736 (124) es 4. Sin embargo, los sistemas de logaritmos de uso frecuente son: base 10 base 2.71828183
log10 x o simplemente log x loge x o simplemente ln x, siendo e = 2.71828183
MATEMATICAS FINANCIERAS CON EXCEL Y MATLAB
4
Los primeros se denominan de base 10, decimales o comunes y los segundos logaritmos naturales o neperianos, de los que la base se simboliza por el número irracional e. Si la base es diferente, se indica como subíndice: logb. Es decir, para los logaritmos de base 10 y naturales, la notación utilizada es: log x y ln x; para calcular el antilogaritmo normalmente se tiene los símbolos 10x y ex, respectivamente. Para realizar operaciones con logaritmos, se debe escoger una sola base, cualquiera de ellas; para todas las operaciones matemáticas los resultados finales serán iguales independientemente de la base utilizada. No se debe mezclar operaciones con logaritmos de diferente base, los resultados serán errados. El logaritmo de cero no existe y no se puede determinar logaritmos de números negativos. Los logaritmos entre 0 y 1 son negativos: NUMERO 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
log -1.000000 -0.698970 -0.522879 -0.397940 -0.301030 -0.221849 -0.154902 -0.096910 -0.045757
NUMERO 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
ln -2.302585 -1.609438 -1.203973 -0.916291 -0.693147 -0.510826 -0.356675 -0.223144 -0.105361
u con la expresión logb u / logb v. v Los exponentes también pueden ser números no enteros, por tanto siempre es posible expresar como una potencia de 10, así tenemos los siguientes ejemplos:
No confundir la expresión la expresión logb
1000 1267
= =
103 por tanto 103.1027 por tanto
log 1000 = 3 log 1267 = 3,1027
Si se usa logaritmos naturales, es decir base e = 2.71828183, los valores de los logaritmos (exponentes) son diferentes: 1000 1267
= =
e 6.90775 por tanto e 7.14440 por tanto
ln 1000 = 6.90775 ln 1267 = 7.14440
Ejemplos de logaritmos de diferentes bases:
5
LOGARITMOS
LOGARITMOS BASE 10
LOGARITMOS BASE e
LOGARITMOS BASE 2 0 LOG2 0 =
10^0 = 10^1 =
1 LOG 1 = 10 LOG 10 =
0 e^0 = 1 e^1 =
1.000000 ln 1 = 2.718282 ln 2.718282 =
0 2^0 = 1 2^1 =
10^2 = 10^3 = 10^4 =
100 LOG 100 = 1000 LOG 1000 = 10000 LOG 10000 =
2 e^2 = 3 e^3 = 4 e^4 =
7.389056 ln 7.389056 = 20.085537 ln 20.08554 = 54.598150 ln 54.59815 =
5 e^5 = 148.413159 ln 148.4132 = 6 e^6 = 403.428793 ln 403.4288 =
10^5 = 100000 LOG 100000 = 10^6 = 1000000 LOG 1000000 =
0
2 2^2 = 3 2^3 = 4 2^4 =
2 LOG2 2 = 4 LOG2 4 = 8 LOG2 8 =
1 2 3
16 LOG2 16 =
5 2^5 = 6 2^6 =
32 LOG2 32 = 64 LOG2 64 =
4 5 6
El logaritmo de un número diferente de 1, cambia si corresponde a diferentes bases
NÚMERO
LOG 10 1
LN
LOG 2
LOG 4
LOG 5
0,000000
0,000000
0,000000
0,000000
0,000000
10
1,000000
2,302585
3,321928
1,660964
1,430677
100
2,000000
4,605170
6,643856
3,321928
2,861353
1.000
3,000000
6,907755
9,965784
4,982892
4,292030
10.000
4,000000
9,210340
13,287712
6,643856
5,722706
100.000
5,000000
11,512925
16,609640
8,304820
7,153383
1.000.000
6,000000
13,815511
19,931569
9,965784
8,584059
1.5 LEYES DE LOS LOGARITMOS Si suponemos que "u" y "v" son números positivos, las leyes aplicables a los logaritmos son: 1.5.1 logb uv logb u logb v
u logb u logb v v 1.5.3 logb uv v logb u 1.5.2 logb
1.5.4 logb 1 0 por lo tanto 1.5.5 logb b 1 por lo tanto
lne e lne 1
log10 10 log10 1
log12 12 1 1.6 RESOLUCIÓN CON EXCEL Para aplicar logaritmos de base e se selecciona la función LN; para los de base 10 la función LOG 10; y, para los de una base diferente a las anteriores la función LOG, de la categoría Funciones Matemáticas y Trigonométricas.
MATEMATICAS FINANCIERAS CON EXCEL Y MATLAB
6
Para el caso de logaritmos de base e, seleccionamos la función LN:
Como argumento se indica la dirección de la celda con el número para el cual se desea obtener el logaritmo natural:
Al pulsar Aceptar se obtiene el resultado:
7
LOGARITMOS
Para el caso de logaritmos de base 10, seleccionamos la función LOG 10:
Al Aceptar, en la ventana de Argumentos de función, ingresamos la dirección de la celda que contiene el dato:
Al pulsar Aceptar se visualiza el resultado en la celda seleccionada:
Para el caso de logaritmos de cualquier base, seleccionamos la función LOG:
MATEMATICAS FINANCIERAS CON EXCEL Y MATLAB
8
Como argumentos de la función se indica la dirección de la celda del Número para el cual se desea obtener el logaritmo y se registra la Base. Si se omite la base, se asume base 10:
Al pulsar Aceptar se obtiene el resultado:
Para determinar el antilogaritmo natural se selecciona la función EXP:
9
LOGARITMOS
Para determinar el antilogaritmo de base 10 se selecciona la función POTENCIA, como argumentos de función en la casilla de Número se indica la base y en la de Potencia la celda del logaritmo o exponente:
Para el ejemplo del logaritmo de base 12 de 1000, obtuvimos 2,779885. El antilogaritmo con la función POTENCIA es:
1.7 PROPIEDADES QUE RELACIONAN FUNCIONES EXPONENCIALES Y LOGARITMICAS La función exponencial con base "b" y exponente "x" se expresa de la forma: y bx La función exponencial con base "e" y exponente "x" se expresa de la forma: y ex La función logarítmica con base "b" y exponente "x" se expresa de la forma: y log b x La función logarítmica con base "e" y exponente "x" se expresa de la forma: y ln x
MATEMATICAS FINANCIERAS CON EXCEL Y MATLAB 10
Propiedades: 1.7.1 e lnx x
en donde
x>0
1.7.2 ln ex x para cualquier número x Gráfica que expresa la relación entre la función exponencial y la función logarítmica: Ver pág. 161 libro de Millar (maestría economía) Estas propiedades permiten resolver ecuaciones con exponenciales y logaritmos.
Ejercicio 1.1
Resolver mediante logaritmos de base 10 la siguiente multiplicación: 1000*100 Solución: log 1000 = 3 log 100 = 2
ya que 1000 = 103 ya que 100 = 102
Sumamos los logaritmos (exponentes) : 3 + 2 = 5 A continuación, el logaritmo resultante (exponente final) aplicamos a la base y realizamos la operación matemática respectiva: 105 = 100000 Para este último paso nos referimos normalmente a encontrar el antilogaritmo de 5, por tanto, determinar el antilogaritmo de un número, es averiguar el resultado de elevar la base utilizada de los logaritmos al número indicado.
Ejercicio 1.2
Resolver mediante logaritmos la siguiente operación matemática: y = 340*678 Solución con logaritmos de base 10: log y = log 340 + log 678 =2.53147892+2.83122969 =5.36270861 Encontramos el antilogaritmo 105.36270861 = 230520 Solución: con logaritmos naturales ln y = ln 340 + ln 678 = 5.82894562 + 6.51914729 = 12.3480929 Encontramos el antilogaritmo e12.3480929 = 230520
11
LOGARITMOS
Despejar x de: y + 142 = (z + 345)x
Ejercicio 1.3 Solución: log(y + 142) = log((z + 345)x) log(y + 142) = x*log(z + 345) x*log(z + 345) = log(y + 142) x = log(y + 142) / log(z + 345)
Ejercicio 1.4
Resolver con logaritmos de base 10: y = 45 * 5,58 Solución: log y = 5*log4 + 8*log5,5 log y = 5*0,602060 + 8*0,740363 log y = 3,0103 + 5,922901 log y = 8,933201 El antilogaritmo con la función 10x: y = 857.435.524
Ejercicio 1.5
Resolver con logaritmos de base 8: y = 45 * 5,58 Solución: log8 y = 5*log84 + 8*log85,5 log8 y = 5*0,666667 + 8*0,819811 log8 y = 3,333333 + 6,558484 log8 y = 8,891818 El antilogaritmo con la función potencia 8x: y = 857.435.524
Resolver con logaritmos de base ℮: y = 45 * 5,58
Ejercicio 1.6 Solución: ln y = 5*ln4 + 8 *ln 5,5 ln y = 5*1,386294 + 8*1,704748 ln y = 6,931472 + 13,637985 ln y = 20,569457 El antilogaritmo con la función ℮x: y = 857.435.524
Ejercicio 1.7
Resolver con logaritmos de base 10: y = √16 * 250⅔
MATEMATICAS FINANCIERAS CON EXCEL Y MATLAB 12
Solución: log y = 1⁄2log16 + 2/3log 250 log y = 1⁄2*1,204120 + 2/3*2,397940 log y = 2,200687 El antilogaritmo con la función 10x: y = 158,74
Ejercicio 1.8
Utilizando logaritmos de base 10 despejar "n" de la ecuación: S P (1 i) n
S n P (1 i ) S (1 i )n P n log(1 i) log S log P n
Ejercicio 1.9
log S log P log(1 i )
n Utilizando logaritmos de base ℮ despejar "n" de la ecuación: S P (1 i )
S (1 i )n P n ln(1 i ) ln S ln P n
Ejercicio 1.10
ln S ln P ln(1 i )
n Utilizando logaritmos de base 10 despejar "i" de la ecuación: S P (1 i)
S (1 i )n P n log(1 i) log S log P log S log P n Para obtener el valor de la tasa de interés se requiere determinar el antilogaritmo. log(1 i )
Ejercicio 1.11
Utilizando logaritmos de base ℮ despejar "j∞" de la ecuación: S P * e J n P * e J n S
13
LOGARITMOS
S P j n ln e ln S ln P
e J n
j
Ejercicio 1.12
ln S ln P n
Resolver la ecuación: 2ex 2 8 Simplificando: e x 2 4 Aplicando logaritmos:
Ejercicio 1.13
ln ex 2 ln 4 (x 2) lne ln4 (x 2) ln 4 x 2 ln 4 x 0.613706
Si log 3 = 0.477121 y log 4 = 0.602060, determinar el valor de los siguientes logaritmos: a) log 12 b) log 16 c) log (4/3) Solución: a) log 12 = log 3 + log 4 log 12 = 1,079181 b) log 16 log(16 )1/ 2
1 1 log 16 (log 4 log 4 ) (0 .602060 0 .602060 ) 0 .602060 2 2 4 c) log log4 log3 3 4 log 0 .602060 0.477121 0 .124939 3
Ejercicio 1.14
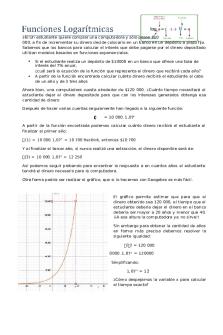
Graficar la función exponencial y 3x , para valores de -3 a 3, con variaciones de una unidad.
MATEMATICAS FINANCIERAS CON EXCEL Y MATLAB 14 Valores x y3
Ejercicio 1.15
-3 0.03703704
-2 0.11111111
-1 0.33333333
0 1
1 3
2 9
3 27
Graficar la función logarítmica y log 3 x , para valores de 0.5 a 4, con incrementos de 0.5 Valores
y log3 x
0.5 -0.630930
1 0.000000
1.5 0.369070
2 0.630930
2.5 0.834044
3 1.000000
3.5 1.140314
4 1.261860...
Similar Free PDFs

Cap 1 logaritmos - Nota: 10
- 14 Pages

Evidencia 1 - Nota: 10
- 10 Pages

Laboratorio 1 - Nota: 10
- 32 Pages

Laboratorio 1 - Nota: 10
- 6 Pages

Software 1 - Nota: 10
- 18 Pages

Gastro 1 - Nota: 10
- 1 Pages

Entregable 1 - Nota 10
- 4 Pages

Logaritmos
- 6 Pages

Logaritmos
- 59 Pages
Logaritmos - Lecture notes 1
- 3 Pages

Actividad 10 - Nota: 10
- 7 Pages

1- Arquitetura Naval - Nota: 10
- 128 Pages

CASO 1 Ecoalf - Nota: 10
- 5 Pages

Foro Humanismo 1 B 1 - Nota: 10
- 3 Pages

Spring- Spring 1-1 - Nota: 10
- 10 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu
