Comparer des distributions d\'effectifs le test de X2 (chi2) PDF

| Title | Comparer des distributions d\'effectifs le test de X2 (chi2) |
|---|---|
| Course | Biostatistiques |
| Institution | Université de Franche-Comté |
| Pages | 12 |
| File Size | 1.2 MB |
| File Type | |
| Total Downloads | 79 |
| Total Views | 136 |
Summary
Cours de biostatistique.
Niveau de 2e année de licence BBCP, semestre 3....
Description
Co Com mpa parrer d de es di disstr trib ib ibut ut utio io ions ns d’ d’ef ef efffectif ctifss : le te test st de X2 (chi (chi2) 2) 1. Ex Exem em emple ple de tabl tablea ea eau u de con contigen tigen tigence ce
Deux variables : Discrètes (= discontinues) : Groupe sanguin {O, A, B, AB}
Rhésus {+ ; -}
Qualitatives : O, A, B, AB ne peuvent être réciproquement ordonnés… De même que + et -.
2. Du ttablea ablea ableau u de cont continge inge ingenc nc nce e aaux ux dist distribu ribu ribution tion tionss de pr prob ob obab ab abilités ilités
p(Rhésus+ et groupe sanguin O) = 0.37 p(Rhésus+) = 0.841 etc.
3. Ra Rappe ppe ppell : ccalcu alcu alculls de p pro ro roba ba bab bilités 1. Axiome des probabilités totales
Soit E1 et E2 deux issues possibles d’une même expérience aléatoire, si E1 et E2 sont mutuellement incompatibles (c’est-à-dire qu’ils ne peuvent pas se produire en même temps), on peut écrire :
p(E1ou E2) = p(E1) + p(E2)
2. Axiome des probabilités composées Soit E1 et E2 deux résultats possibles d’une même expérience aléatoire, mais E1 et E2 étant compatibles : l’apparition de E1 n’exclut pas celle de E2. Si les deux évènements sont indépendants (cad si la réalisation de E1 ne modifie pas la probabilité de celle de E2), on peut écrire que :
p(E1et E2) = p(E1) x p(E2)
4. Object bjectif if d d’u ’u ’un n tes testt de X2 Le test de X2 consiste à mesurer l’écart entre : Des effectifs observés Et des effectifs attendus (dites parfois « théoriques ») = ceux calculés sous l’hypothèse d’indépendance des variables = sous l’hypothèse que s’appliquent les axiomes des probabilités totales et composées … et à tester si cet écart est suffisamment faible pour être imputable aux fluctuations aléatoires d’échantillonnage. Son domaine d’utilisation est celui des tableaux de contingence.
I.
Princ pour tab rincipe ipe de cal calcul cul d d’un ’un te test st de X2 pour tableau leau de con continge tinge tingencec ncec de k éch échanti anti antillons llons in indép dép dépend end endants ants
On a vacciné une population humaine avec deux vaccins BCG A et B et on a observé les réactions induites : Sous forme d’effectifs :
Sous forme de pourcentage :
Hypothèse nulle : les 2 variables sont indépendantes :
Ri : total de la colonne Ci : total de la ligne (juste retenir la formule de Chi2, ce tableau en est l’équivalent.)
Notion de degrés de liberté (ddl, df) Le degré de liberté = nombre de composante indépendantes utilisées dans le calcul
On peut écrire le ddl simplement ddl = (k-1)(r-1) !
On ne comptabilise que ce qu’il y a en vert sur le tableau. Si on se trompe de valeur seuil, c’est comme si on acceptait H0.
Comment lire la table ?
Plus le seuil sera petit et plus la valeur sera grande. Conditions d’application : les règles de Cochran (1954)
Si ddl > 1
80% des cellules doivent présenter des fréquences attendues dépassant la valeur 5 Aucune cellule ne doit avoir une fréquence attendue inférieure à 1.
Si ces conditions ne sont pas respectées, il est peut-être possible (si cela a biologiquement un sens) de regrouper des lignes et/ou des colonnes pour avoir un tableau de contingence conforme.
- Si ddl = 1 (tableau de contingence 2x2) Si l’effectif est indérieur à 20 : test des probabilités exactes de Fisher Si 20 ≤n ≤40, et toutes les fréquences théoriques sont supérieures ou égales à5, on utilise la correction de continuité de Yates:
Si 20 ≤n < 40 et si certaines fréquences théoriques s'avèrent inférieures à 5, il faut appliquer test des probabilités exactes de Fisher, ou le test G. Si n > 40, le test de X2est valide à condition que les proportions étudiées ne soient pas voisines de 0 ou de 1. Si tel est le cas, il faut appliquer le test des probabilités exactes de Fisher.
On réalise plusieurs épreuves successives. Si les réalisations de ces épreuves sont indépendantes, alors la distribution des succès (et des échecs) correspond à une loi de distribution binomiale. La distribution de probabilité de la loi binomiale est fournie par le développement du binôme (p+q)n, avec n, le nombre d'épreuves. Si on effectue 2 épreuves successives, quelles sont les probabilités d’avoir 0, 1 et 2 rats atteignant le point noir ?
(p+q)2 = p2 + 2pq + q2...
Similar Free PDFs
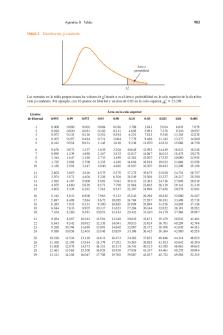
Tabla chi2
- 2 Pages

Nota de prensa termindad x2
- 2 Pages
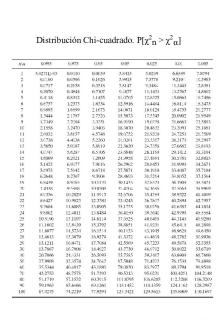
Tabla chi2
- 1 Pages

Le cycle des roches
- 17 Pages

Le monde des Idées
- 6 Pages

Le départ des volontaires
- 3 Pages

Le consentement des époux
- 2 Pages

Le Gouvernement des langues
- 44 Pages

Le-pluriel-des-
- 3 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu






