Parte I - IA Clásica - Resolución de problemas PDF

| Title | Parte I - IA Clásica - Resolución de problemas |
|---|---|
| Author | Fertry .. |
| Course | Inteligencia Artificial (IC) |
| Institution | Universidad de Sevilla |
| Pages | 7 |
| File Size | 359.9 KB |
| File Type | |
| Total Downloads | 1 |
| Total Views | 138 |
Summary
Download Parte I - IA Clásica - Resolución de problemas PDF
Description
fertry Inteligencia Artificial Parte I: IA Clásica Resolución de Problemas: Problemas de Satisfacción de Restricciones – PSR
La resolución de muchos problemas está sujeta a poder descomponerlos en conjuntos de restricciones. La representación y resolución de problemas de satisfacción de restricciones (PSR) se encuentran dentro de los llamados problemas NP (complejidad computacional excesiva para su resolución). La idea de PSR es representar un problema mediante la declaración de restricciones sobre el área del problema (espacio de posibles soluciones) y, consecuentemente, encontrar soluciones que satisfagan todas las restricciones. Diferenciamos dos conjuntos: aquellos problemas con dominios finitos y otros con dominios infinitos o mucho más complejos. (Nosotros nos centramos en los problemas de dominio finito que constan de un conjunto determinado de variables, un dominio de valores finito para cada variable y un conjunto de restricciones).
Ejemplo: “Coloración de mapas” --> dado un mapa dividido en regiones, el objetivo es colorear cada región de un color de forman que las regiones adyacentes tengan siempre colores distintos. --> para modelar este problema mediante PSR se asocia una variable a cada región del mapa cuyo dominio, es el conjunto de colores disponibles y para cada par de regiones contiguas, se añade una restricción sobre los valores que puede tomar.
Metodología de PSR 1. Modelar (representar) el problema como un problema de satisfacción de restricciones: expresar el problema (como en el ejemplo anterior) mediante un conjunto de variables, dominios en los que toman valores y restricciones sobre esas variables. 2. Procesar las restricciones: dos formas: a. Técnicas de consistencia: basadas en la eliminación de valores inconsistentes de los dominios de las variables (que no verifican las restricciones). b. Algoritmos de búsqueda: se basan en la exploración sistemática del espacio de soluciones hasta encontrar una (o no) que verifique las restricciones.
1 fertry
fertry Modelización (representación) de PSR Ejemplo: “send + more = money” --> a cada letra {s,e,n,d,m,o,r,y} hay que asignar un nº distinto del conjunto {0…9} de forma que satisfaga que send + more = money --> para comenzar asignamos una variables a cada letra (que ya son letras) todas ellas con un dominio claro {0…9} y aplicamos unas restricciones tal que: 1. Todas las variables toman valores distintos 2. send + more = money
de esta forma las restricciones quedan como:
103(s+m)+102(e+o)+10(n+r)+d+e = 104m+103o+102n+10e+y con lo que se ve que no es satisfactorio ya que:
s≠e, s≠n, ..., r≠y Para resolverlo, vamos a descomponer la ecuación anterior en una colección de pequeñas restricciones. Para ello introducimos el concepto de “acarreo”:
de esta forma, la suma con acarreo queda como:
e+d=y+10c1 c1+n+r=e+10c2 c2+e+o=n+10c3 c3+s+m=10m+o al quedar restricciones más pequeñas, estas pueden comprobarse durante la búsqueda de forma más sencilla y reduciendo el espacio de búsqueda.
Formalización de PSR Un problema de PSR es una terna (X, D, C) donde: 1. X es un conjunto de n variables {x1, …. , xn}. 2. D = {D1, …., Dn} es un vector de dominios. 3. C es un conjunto finito de restricciones. Cada restricción está definida sobre un conjunto de k variables por medio de un predicado.
2 fertry
fertry Una asignación de variables (x,a) es un par variable-valor que representa la asignación del valor a la variable x. Una asignación de un conjunto de variables es una tupla de pares ordenados. Esta tupla se dice “localmente consistente” si satisface todas las restricciones. Una solución PSR es una asignación de valores a todas las variables de forma que satisfagan todas las restricciones. Es decir, una solución es una tupla consistente que contiene TODAS las variables del problema. Una solución parcial es una tupla consistente que consistente que contiene algunas de las variables del problema. Diremos que un problema es consistente si existe al menos una solución. Para representar variables utilizamos letras del alfabeto. Para representar restricciones las denotamos como C1…Ck.
Ejemplo: “Las N-reinas” --> dado un tablero de ajedrez del tamaño N * N donde N es el nº de reinas (asumimos que todo el mundo sabe jugar al ajedrez); el problema consiste en disponer a todas las reinas en el tablero de forma que no haya amenazas entre ningún par de ellas. (Recordamos que una reina amenaza a toda su fila, columna y diagonal). 1º representación (Para N=8 --> 64^8 posibles asignaciones y 126 restricciones)
X = {R1,…,RN}
(donde R son las reinas)
D = {(x, y): 1 ≤ x, y ≤ N} (donde x, y es la posición de las reinas) Las restricciones:
a. b. c. d.
xi≠xj, para todo i≠j yi≠yj, para todo i≠j xi−xj≠yi−yj, para todo i≠j xi−xj≠yj−yi, para todo i≠j
(no hay amenaza horizontal) (no hay amenaza vertical) (no hay amenaza en diagonal principal) (no hay amenaza diagonal secundaria)
2º representación (Para N=8 --> 64^2 posibles asignaciones y 300 restricciones)
X = {Ri,j: 1 ≤ x, y ≤ N}
(ahora trato las casillas)
D = {0, 1}
(hay o no hay reina en esa casilla)
Las restricciones:
∑i Ri, j≤ 1, para todo 1 ≤ j ≤ N (en cada fila, solo una reina) b. ∑j Ri,j ≤ 1, para todo 1 ≤ i ≤ N (en cada columna, solo una reina) c. ∑(i,j)∈D Ri,j ≤ 1, para toda D diagonal (en cada diagonal, solo una reina)
a.
3º representación (usando predicados lógicos)
X = {Ri,j: 1 ≤ x, y ≤ N}
(para cada casilla)
D = {0, 1}
(hay o no hay reina en esa casilla)
Las restricciones: a.
(Ri,j → ¬Ri,j′), para todo j′≠j 3
fertry
fertry
(Ri,j → ¬Ri′,j), para todo i′≠i c. (Ri,j → ¬Ri+k,j+k), para todo 1 ≤ i + k, j + k ≤ N d. (Ri,j → ¬Ri+k,j−k), para todo 1 ≤ i + k, j − k ≤ N b.
4º representación (Para N=8 --> 8^8 y 80 restricciones; haciendo uso del conocimiento implícito de que va a haber una, y solo una, reina en cada columna)
X = {Ri: 1 ≤ i ≤ N}
(donde R son las reinas)
D = {1,…,N}
(la columna que ocupa cada reina)
Las restricciones:
Ri≠Rj, para todo i≠j b. |Ri−Rj| ≠ |i−j|, para todo i≠j a.
(saltamos la consistencia de un PSR y vamos directamente a Heurística)
Heurísticas Seleccionar el orden correcto de las variables, de los valores y de las restricciones puede mejorar notablemente la eficiencia de la resolución. Ordenación de variables: generalmente las heurísticas de ordenación de variables tratan de seleccionar antes las variables que más restringen a las demás. La ordenación de variables puede ser estática y dinámica: Heurísticas de ordenación de variables estáticas: a. Minimum Width (MW): la anchura de la variable X es el nº de variables que están antes de X de acuerdo con un orden dado y que son adyacentes a X. Las variables que están al principio de la ordenación son las más restringidas y las variables que están al final las menos restringidas. b. Maximun Degree (MD): ordena las variables en orden decreciente según el grafo de restricciones. El grado de un nodo se define como el nº de nodos adyacente a él. c. Maximun Cardinality (MC): selecciona la primera variable aleatoriamente y después, en cada paso, selecciona la variable adyacente al conjunto más grande. Heurísticas de ordenación de variables dinámicas: a. Principio del 1º fallo (FF): consiste en probar primero donde es más probable que falle. De esta forma se identifican antes las situaciones sin salida. En cada caso seleccionamos la variable más restringida. b. Minimun Remaining Values (MRV): trata de hacer lo mismo que FF pero con un dominio más reducido para cada variable.
4 fertry
fertry Ordenación de valores: la idea es seleccionar el valor de la variable que más probabilidad tenga de llevarnos a una solución. Heurística de ordenación de variables: a. Heurística min-conflicts: ordena los valores de acuerdo a los conflictos en los que estos están involucrados con las variables instanciadas.
Resolución de Problemas: Problemas de Búsqueda y Planificación
Definimos la resolución de problemas como el proceso que, partiendo de una situación inicial y utilizando un conjunto de procedimientos/reglas/acciones seleccionados a priori, es capaz de explicitar el conjunto de pasos que nos llevan a una situación posterior que llamamos solución. Para poder modelar sistemas que nos lleven a esas soluciones, es necesario poder expresar las características de los problemas usando un lenguaje formal, que luego dará lugar a algoritmos.
Una de las aproximaciones más sencillas para formalizar un problema es el llamado espacio de estados. Definimos un estado como la representación de los elementos que describen el problema en un instante dado. No existen directrices claras sobre que incluir en el estado en cada caso, pero, aunque a priori pueda parecer necesario almacenar toda la información posible, esto puede dar lugar a imposibles desde el punto de vista del almacenamiento y procesado computacional. Decimos que debe existir un equilibrio entre el ahorro de recursos de almacenamiento para la descripción de los estados y la necesidad de tener suficiente información almacenada como para poder resolver el problema. Este problema se conoce como la Teoría de la Representación. Llamamos “modelar el problema” a transformar el problema original en un espacio de estados manipulable por medios automáticos.
Problema de búsqueda básico Un problema de búsqueda básico es una tupla (X, S, G, d) donde: 1. X es un conjunto de estados (espacio de estados). 2. S ⊆ X es un conjunto NO vacío de estados iniciales (pueden ser más de uno). 3. G ⊆ X es un conjunto NO vacío de estados finales (pueden ser más de uno). 4. d : X → P(x) es una función de transición. Para cada x ∈ X, d(x) determina el conjunto de estados sucesores de x. 5 fertry
fertry Si imaginamos el llamado espacio de estados como un terreno sobre el que nos movemos; partimos de un punto (estado inicial) y debemos buscar un camino para llegar a otro punto (estado final). Una vez fijada esta idea, seguimos estos pasos: 1. Dar una representación al problema, es decir, definir un espacio de estados. Esta elección no es única. (La capacidad para obtener una representación más adecuada se denomina perspicacia). 2. Especificar uno o más estados iniciales. 3. Especificar uno o más estados finales (objetivos). (Es posible que en lugar de especificar un estado final se especifique un objetivo a cumplir). 4. Definir reglas a partir de las acciones disponibles. El conjunto de reglas será la que defina la función de transición del sistema. 5. El problema se resuelve usando las reglas en combinación con una estrategia de control. Una buena estrategia de control debe establecer un orden de aplicación para las reglas y debe resolver los posibles conflictos que aparezcan. 6. Dependiendo de la estrategia utilizada, es posible definir una función de coste que indique cuanto cuesta aplicar una regla determinada de forma que podamos comparar caminos.
Planificación En muchos casos no queremos simplemente ir de A a B sino obtener la sucesión que nos lleva de un punto a otro. Esto se conoce como Problema de Planificación y, a la sucesión que buscamos, se le denomina Plan. Tal y como sucede con los problemas de búsqueda, es importante dar una representación formal del mundo y de las acciones que se pueden aplicar a él. Es recomendable considerar: a. Un espacio de estado finito. b. Estados completamente observables y determinados (esto es, no hay estados en incertidumbre). c. Acciones deterministas (la aplicación de una acción devuelve un único estado posible). d. Tiempo implícito (las acciones tardan el mismo tiempo en ejecutarse). Ejemplo: “Puzle de piezas deslizantes” --> donde el objetivo es deslizar las piezas haciendo uso de un único hueco hasta que queden en el orden deseado. El tablero cuenta con n x m cuadrículas y n x m – 1 piezas enumeradas consecutivamente y un hueco.
6 fertry
fertry El espacio de estados (X) describe todas las posibles combinaciones de las piezas y el hueco. El conjunto de estados iniciales (S) en este caso es todo el espacio: S = X; y el conjunto de estados finales es único: cuando todas las piezas están en su posición correcta y el hueco al final (como en la figura). La función de transición describe el cambio que resulta de mover, en un estado cualquiera, el hueco hacia cualquiera de las 4 direcciones (en el caso de los bordes y esquinas solo hay 3 o 2 direcciones respectivamente). Lo que buscamos aquí, como comentábamos antes, no es el estado final (previamente conocido) sino el camino que nos lleva a él.
Nótese como un puzle de 3x3 da un nº posible de estados de 9! = 362880 (que maravilla Paco). Este tamaño, aunque enorme, permite hacer una búsqueda exhaustiva para encontrar el camino haciendo uso de la capacidad de los ordenadores actuales. Sin embargo, un puzle de 4x4 = 16! = 2x10^13 sería una barbaridad demasiado grande para una búsqueda exhaustiva. Necesitamos otras estrategias de búsqueda (siguiente apartado del tema I).
Criterios de evaluación de algoritmos (estrategias) 1. Complejidad en el tiempo: se puede medir como el nº de veces que se aplica la función de transición para encontrar la solución. 2. Complejidad en el espacio: se puede medir como la cantidad de espacio de almacenamiento necesario para encontrar la solución. 3. Completitud: si existe solución ¿garantiza dicho algoritmo que se alcanzará? 4. Optimalidad: si existen múltiples soluciones, ¿garantiza dicho algoritmo que se encontrará la mejor?
Representación (universal) Los algoritmos (los que vamos a estudiar) tienen un espacio de búsqueda en forma de grafo dirigido. Cada nodo del grafo representa uno de los estados del espacio y dos nodos conectados supone que existe una forma de ir de uno a otro mediante la función de transición.
7 fertry...
Similar Free PDFs

Problemas Parte II
- 1 Pages

problemas i dureza
- 4 Pages

DP - Parte Especial I
- 23 Pages

Instrumental Cirugía Parte I
- 12 Pages
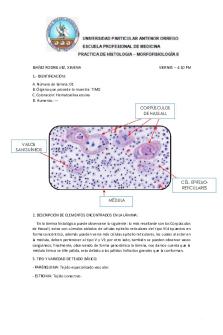
Sistema Linfático Parte I
- 2 Pages

Nomenclatura Parte I-UTP
- 5 Pages

ANTROPOLOGÍA JURÍDICA PARTE I
- 6 Pages

Macro Sebenta Parte I
- 46 Pages
Popular Institutions
- Tinajero National High School - Annex
- Politeknik Caltex Riau
- Yokohama City University
- SGT University
- University of Al-Qadisiyah
- Divine Word College of Vigan
- Techniek College Rotterdam
- Universidade de Santiago
- Universiti Teknologi MARA Cawangan Johor Kampus Pasir Gudang
- Poltekkes Kemenkes Yogyakarta
- Baguio City National High School
- Colegio san marcos
- preparatoria uno
- Centro de Bachillerato Tecnológico Industrial y de Servicios No. 107
- Dalian Maritime University
- Quang Trung Secondary School
- Colegio Tecnológico en Informática
- Corporación Regional de Educación Superior
- Grupo CEDVA
- Dar Al Uloom University
- Centro de Estudios Preuniversitarios de la Universidad Nacional de Ingeniería
- 上智大学
- Aakash International School, Nuna Majara
- San Felipe Neri Catholic School
- Kang Chiao International School - New Taipei City
- Misamis Occidental National High School
- Institución Educativa Escuela Normal Juan Ladrilleros
- Kolehiyo ng Pantukan
- Batanes State College
- Instituto Continental
- Sekolah Menengah Kejuruan Kesehatan Kaltara (Tarakan)
- Colegio de La Inmaculada Concepcion - Cebu







